
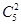 =10種結果,其余的三個盒子與小球的編號不同,則第一個球有兩種選擇,另外兩個球的位置確定,共有2種結果,相乘得到結果.解:由題意知本題是一個排列、組合及簡單計數問題,有且只有兩個小球的編號與盒子號一致,則首先從5個號碼中,選出兩個號碼,有
=10種結果,其余的三個盒子與小球的編號不同,則第一個球有兩種選擇,另外兩個球的位置確定,共有2種結果,相乘得到結果.解:由題意知本題是一個排列、組合及簡單計數問題,有且只有兩個小球的編號與盒子號一致,則首先從5個號碼中,選出兩個號碼,有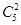 =10種結果,其余的三個小球與盒子的編號不同,則第一個小球有兩種選擇,另外兩個小球的位置確定,編號不同的放法共有2種結果,根據分步計數原理得到共有10×2=20種結果,故答案為A
=10種結果,其余的三個小球與盒子的編號不同,則第一個小球有兩種選擇,另外兩個小球的位置確定,編號不同的放法共有2種結果,根據分步計數原理得到共有10×2=20種結果,故答案為A

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com