【題目】下列關于算法的敘述中正確的是( )
A. —個算法必須能解決一類問題 B. 求解某個問題的算法是唯一的
C. 算法不能重復使用 D. 算法的過程可以是無限的
長江作業本同步練習冊系列答案科目：高中數學 來源： 題型：
【題目】某城市要建成宜商、宜居的國際化現代新城，該城市的東城區、西城區分別引進8甲廠家，現對兩個區域的16個廠家進行評估，綜合得分情況如莖葉圖所示.
（1）根據莖葉圖判斷哪個區域廠家的平均分較高；
（2）規定85分以上（含85分）為優秀廠家，若從該兩個區域各選一個優秀廠家，求得分差距不超過5分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
有如下性質：如果常數
，那么該函數在
上是減函數，在
上是增函數．
（1）已知
，利用上述性質，求函數
的單調區間和值域；
（2）對于（1）中的函數
和函數
，若對任意
，總存在
，使得
成立，求實數
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于在區間
上有意義的兩個函數
與
，如果對任意的
，均有
，則稱
與
在
上是接近的，否則稱
與
在
上是非接近的.現在有兩個函數
與
，現給定區間
.
（1）若
，判斷
與
是否在給定區間上接近；
（2）是否存在
，使得
與
在給定區間
上是接近的；若存在，求
的取值范圍；若不存在，請說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了準備里約奧運會的選拔，甲、乙兩人進行隊內射箭比賽，各射4支箭，兩人4次所得環數如下：（最高為10環）
甲 | 6 | 6 | 9 | 9 |
乙 | 7 | 9 |
|
|
（Ⅰ）已知在乙的4支箭中隨機選取1支時，此支射中環數小于6環的概率不為零，且在4支箭中，乙的平均環數高于甲的平均環數，求
的值；
（Ⅱ）如果
，
，從甲、乙兩人的4次比賽中隨機各選取1次，并將其環數分別記為
，
，求
的概率；
（Ⅲ）在4次比賽中，若甲、乙兩人的平均環數相同，且乙的發揮更穩定，寫出
的所有可能取值．（結論不要求證明）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖所示，矩形
和矩形
所在平面互相垂直，
與平面
及平面
所成的角分別為
，
，
、
分別為
、
的中點，且
.
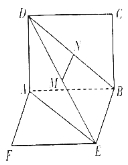
（1）求證：
平面
；
（2）求線段
的長；
（3）求二面角
的平面角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖（1）,在直角梯形ABCP中,AP∥BC,AP⊥AB,AB=BC=
AP=2,D是AP的中點,E,F,G分別是PC,PD,CB的中點,將△PCD沿CD折起,使點P在平面ABCD內的射影為點D,如圖（2）．
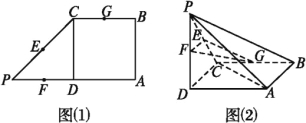
（1）求證:AP∥平面EFG;
（2）求三棱錐P-ABC的體積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】“金導電、銀導電、銅導電、錫導電，所以一切金屬都導電”．此推理方法是( )
A. 完全歸納推理 B. 歸納推理 C. 類比推理 D. 演繹推理
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
