Question

【題目】如圖所示，矩形和矩形所在平面互相垂直，與平面及平面所成的角分別為，，、分別為、的中點(diǎn)，且.

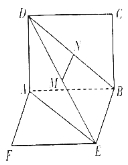
（1）求證：平面；

（2）求線段的長；

（3）求二面角的平面角的正弦值.

Answer 1

【答案】（1）證明見解析；（2）；（3）.

【解析】

試題分析：（1）由面面垂直的性質(zhì)定理易得面；由中位線定理可得，所以有面；（2）利用直角三角形中的邊角關(guān)系求得，在中,由勾股定理求得的長；（3）過 作于點(diǎn),過作于,連,由三垂線定理可證為所求二面角的平面角,用面積法求出和,由 求得二面角的平面角的正弦值.

試題解析：（1）證明：因?yàn)槊?/span>面，面面，，所以面.

因?yàn)?/span>，分別為，的中點(diǎn)，所以，故面.………………（4分）

（2）由（1）可知為與面所成角，，

在直角三角形中，，，所以.

又面面，面面，

，所以面.

所以為與面所成角，，

因此，在直角三角形中，.

在直角三角形中，.………………（8分）

（3）如圖，過作于點(diǎn)，過作于點(diǎn)，連接.

因?yàn)?/span>面，面，

所以.

又，，所以面，

面，故，

又，，所以面.

面，故，又，

因此為所求二面角的平面角.

在直角三角形中，由面積相等有，得

在直角三角形中，同理可得.

.………………（12分）