
【題目】已知函數![]() ,a∈R.
,a∈R.
(Ⅰ)當a=1時,求曲線y=f(x)在點(0,f(0))處的切線方程;
(Ⅱ)求f(x)的單調區間.
【答案】(Ⅰ)y=0(Ⅱ)單調遞減區間為(-1,-![]() ),單調遞增區間為(-∞,-1),(-
),單調遞增區間為(-∞,-1),(-![]() ,+∞)
,+∞)
【解析】
(Ⅰ)當![]() 時,求出函數
時,求出函數![]() ,利用導數的幾何意義求出
,利用導數的幾何意義求出![]() 處的切線的斜率,利用點斜式求出切線方程;(II)當
處的切線的斜率,利用點斜式求出切線方程;(II)當![]() 時,令
時,令![]() ,得
,得![]() ,
,![]() ,分三種情況①
,分三種情況①![]() ,②當
,②當![]() ,③當
,③當![]() ,討論
,討論![]() 的單調區間.
的單調區間.
(Ⅰ)f(x)的定義域為R,![]() .
.
當a=1時,f′(0)=0,f(0)=0,
所以曲線y=f(x)在點(0,f(0))處的切線方程為y=0.
(Ⅱ)f′(x)=aex(x+1)-x-1=(x+1)(aex-1).
(1)當a≤0時,aex-1<0,
所以當x>-1時,f′(x)<0;當x<-1時,f′(x)>0.
所以f(x)的單調遞增區間為(-∞,-1),單調遞減區間為(-1,+∞).
(2)當a>0時,令f′(x)=0,得x1=-1,x2=-lna.
①當-lna=-1,即a=e時,f′(x)≥0,
所以f(x)的單調遞增區間為(-∞,+∞),無單調遞減區間;
②當-lna<-1,即a>e時,
當-lna<x<-1時,f′(x)<0;當x<-lna或x>-1時,f′(x)>0.
所以f(x)的單調遞減區間為(-lna,-1),單調遞增區間為(-∞,-lna),(-1,+∞);
③當-lna>-1,即0<a<e時,
當-1<x<-lna時,f′(x)<0;當x<-1或x>-lna時,f′(x)>0.
所以f(x)的單調遞減區間為(-1,-lna),單調遞增區間為(-∞,-1),(-lna,∞).


科目:高中數學 來源: 題型:
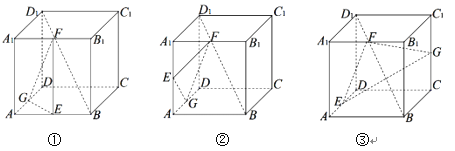
【題目】如圖,在下列三個正方體![]() 中,
中,![]() 均為所在棱的中點,過
均為所在棱的中點,過![]() 作正方體的截面.在各正方體中,直線
作正方體的截面.在各正方體中,直線![]() 與平面
與平面![]() 的位置關系描述正確的是
的位置關系描述正確的是
A. ![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②③
的有且只有②③
B. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有①
的有且只有①
C. .![]() 平面
平面![]() 的有且只有①;
的有且只有①;![]() 平面
平面![]() 的有且只有②
的有且只有②
D. ![]() 平面
平面![]() 的有且只有②;
的有且只有②;![]() 平面
平面![]() 的有且只有③
的有且只有③
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),以坐標原點為極點,
),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和極坐標方程;
的普通方程和極坐標方程;
(2)若![]() 與
與![]() 相交于
相交于![]() 、
、![]() 兩點,且
兩點,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|ax-2|,不等式f(x)≤4的解集為{x|-2≤x≤6}.
(1)求實數a的值;
(2)設g(x)=f(x)+f(x+3),若存在x∈R,使g(x)-tx≤2成立,求實數t的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】科研人員在對人體脂肪含量和年齡之間關系的研究中,獲得了一些年齡和脂肪含量的簡單隨機樣本數據,如下表:
| 26 | 27 | 39 | 41 | 49 | 53 | 56 | 58 | 60 | 61 |
| 14.5 | 17.8 | 21.2 | 25.9 | 26.3 | 29.6 | 31.4 | 33.5 | 35.2 | 34.6 |
根據上表的數據得到如下的散點圖.
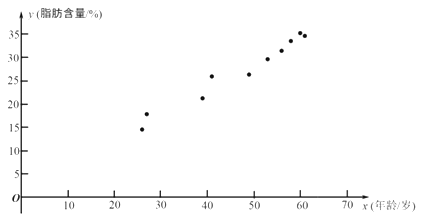
(1)根據上表中的樣本數據及其散點圖:
(i)求![]() ;
;
(i)計算樣本相關系數(精確到0.01),并刻畫它們的相關程度.
(2)若![]() 關于
關于![]() 的線性回歸方程為
的線性回歸方程為![]() ,求
,求![]() 的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
的值(精確到0.01),并根據回歸方程估計年齡為50歲時人體的脂肪含量.
附:參考數據:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
參考公式:相關系數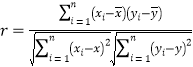
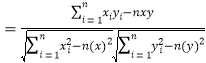
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為
中斜率和截距的最小二乘估計公式分別為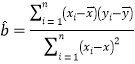 ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com