
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,二面角
,二面角![]() 為
為![]() ,
,![]() 為
為![]() 的中點,點
的中點,點![]() 在
在![]() 上,且
上,且![]()
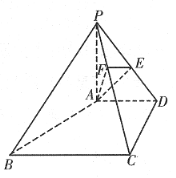
(1)求證:四邊形![]() 為直角梯形;
為直角梯形;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)通過證明![]() ,且
,且![]() 可得四邊形
可得四邊形![]() 為直角梯形;
為直角梯形;
(2)過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,則
,則![]() ,
,![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系
軸,建立如圖所示的空間直角坐標系![]() ,求出面
,求出面![]() 和面
和面![]() 的法向量,求出法向量的夾角即可得二面角
的法向量,求出法向量的夾角即可得二面角![]() 的余弦值.
的余弦值.
(1)證明:因為![]() 平面
平面![]() ,
,![]() ,
,
所以![]()
因為![]() ,且
,且![]() ,
,
所以四邊形![]() 為直角梯形;
為直角梯形;
(2)過點![]() 作
作![]() 的垂線交
的垂線交![]() 于點
于點![]() ,則
,則![]() ,
,![]() ,以
,以![]() 為坐標原點,分別以
為坐標原點,分別以![]() ,
,![]() ,
,![]() 為
為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系
軸,建立如圖所示的空間直角坐標系![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
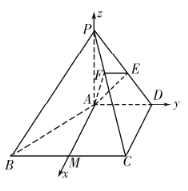
由(1)知![]() ,又
,又![]() ,則
,則![]() 為二面角
為二面角![]() 的平面角,則
的平面角,則![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,
設平面![]() 的法向量
的法向量![]() ,則
,則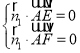 ,即
,即![]()
令:![]() ,則
,則![]() ,
,![]() ,所以
,所以![]() ,
,
又平面![]() 的法向量
的法向量![]() ,
,
所以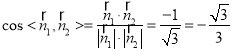 ,
,
由題意知二面角![]() 為鈍角,
為鈍角,
所以二面角![]() 的余弦值為
的余弦值為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】一元線性同余方程組問題最早可見于中國南北朝時期(公元![]() 世紀)的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”問題,原文如下:有物不知數,三三數之剩二,五五數之剩三,問物幾何?即,一個整數除以三余二,除以五余三,求這個整數.設這個整數為
世紀)的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”問題,原文如下:有物不知數,三三數之剩二,五五數之剩三,問物幾何?即,一個整數除以三余二,除以五余三,求這個整數.設這個整數為![]() ,當
,當![]() 時,符合條件的
時,符合條件的![]() 共有( )
共有( )
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面
的底面![]() 為直角梯形,
為直角梯形,![]() ,且
,且![]() ,
,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() 為等邊三角形,
為等邊三角形,![]() 是棱
是棱![]() 上的一點,設
上的一點,設![]() (
(![]() 與
與![]() 不重合).
不重合).
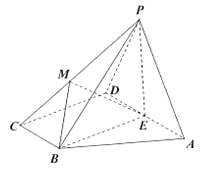
(1)當![]() 時,求三棱錐
時,求三棱錐![]() 的體積;
的體積;
(2)若![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,以坐標原點
中,以坐標原點![]() 務極點,
務極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() ,
,![]()
(1)求曲線![]() ,
,![]() 的直角坐標方程;
的直角坐標方程;
(2)曲線![]() 和
和![]() 的交點為
的交點為![]() ,
,![]() ,求以
,求以![]() 為直徑的圓與
為直徑的圓與![]() 軸的交點坐標.
軸的交點坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據統計調查數據顯示:某企業某種產品的質量指標值![]() 服從正態分布
服從正態分布![]() ,從該企業生產的這種產品(數量很大)中抽取100件,測量這100件產品的質量指標值,由測量結果得到如圖所示的頻率分布直方圖,質量指標值落在區間
,從該企業生產的這種產品(數量很大)中抽取100件,測量這100件產品的質量指標值,由測量結果得到如圖所示的頻率分布直方圖,質量指標值落在區間![]() ,
,![]() ,
,![]() 內的頻率之比為
內的頻率之比為![]() .
.
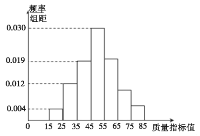
(1)求這100件產品質量指標值落在區間![]() 內的頻率;
內的頻率;
(2)根據頻率分布直方圖求平均數![]() (同一組中的數據用該組區間的中點值作代表);
(同一組中的數據用該組區間的中點值作代表);
(3)若![]() 取這100件產品指標的平均值
取這100件產品指標的平均值![]() ,從這種產品(數量很大)中任取3個,求至少有1個
,從這種產品(數量很大)中任取3個,求至少有1個![]() 落在區間
落在區間![]() 的概率.
的概率.
參考數據:![]() ,若
,若![]() ,則
,則![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,曲線C的參數方程為![]() (α為參數),在以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,點M的極坐標為
(α為參數),在以坐標原點O為極點,x軸的正半軸為極軸的極坐標系中,點M的極坐標為![]() ,直線l的極坐標方程為
,直線l的極坐標方程為![]() .
.
(1)求直線l的直角坐標方程與曲線C的普通方程;
(2)若N是曲線C上的動點,P為線段MN的中點,求點P到直線l的距離的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com