
分析 (Ⅰ)找出滿足條件的m,n的范圍,利用區間長度比求概率;
(Ⅱ)求出滿足條件的m,n的關系式,計算單元區域的面積,利用面積比求概率;
(Ⅲ)利用隨機數模擬的方法,結合滿足條件的隨機次數,利用頻率f=$\frac{{N}_{1}}{N}$,得出概率的近似值.
解答 解:(Ⅰ)m=1,方程x2+x+n2=0有實數根等價于△=1-4n2≥0即$-\frac{1}{2}$≤n≤$\frac{1}{2}$,…(1分)
由幾何概型概率公式得方程有解的概率為P=$\frac{\frac{1}{2}-(-\frac{1}{2})}{1-(-1)}=\frac{1}{2}$.…(3分)
(Ⅱ)方程x2+mx+n2=0有實數根等價于△=m2-4n2≥0.即$\left\{\begin{array}{l}{m+2n≥0}\\{m-2n≥0}\end{array}\right.$或$\left\{\begin{array}{l}{m+2n≤0}\\{m-2n≤0}\end{array}\right.$.
設事件A={方程有實根},則A構成的區域面積為$2×\frac{1}{2}×1×1$=1
…(4分)
(m,n)可看成是平面內的點,試驗的所有結果所構成的區域為Ω={(m,n)|-1≤m≤1,-1≤n≤1},
這是一個邊長為2的正方形區域,面積為4,…(6分)
所以由幾何概性概率告訴的關于x的方程x2+mx+n2=0有實數根的概率p=$\frac{{S}_{A}}{{S}_{Ω}}=\frac{1}{4}$.…(9分)
(Ⅲ)第一步:利用計算器或者計算機產生兩組0到1之間的隨機數:m=RAND,n=RAND;
第二步:統計試驗的總次數N和滿足條件“m2-4n2≥0”的次數N1;
第三步:計算頻率f=$\frac{{N}_{1}}{N}$,得出概率的近似值為f=$\frac{{N}_{1}}{N}$.…(12分)
點評 本題考查了幾何概型的概率求法;關鍵是正確選擇幾何測度,利用公式求概率.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:選擇題
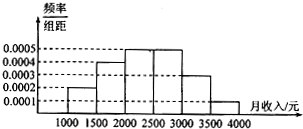 一個社會調查機構就某地居民的月收入調查了10000人,并根據所得數據畫了樣本的頻率分布直方圖(如圖所示).為了進一步分析居民的收入與年齡、學歷、職業等方面的關系,要從這10000人中再用分層抽樣的方法抽出100人作進一步調查,則在[2000,2500]月收入段應抽出( )
一個社會調查機構就某地居民的月收入調查了10000人,并根據所得數據畫了樣本的頻率分布直方圖(如圖所示).為了進一步分析居民的收入與年齡、學歷、職業等方面的關系,要從這10000人中再用分層抽樣的方法抽出100人作進一步調查,則在[2000,2500]月收入段應抽出( )| A. | 10人 | B. | 15人 | C. | 20人 | D. | 25人 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [$\frac{3}{4}$,1) | B. | [$\frac{5}{7}$,1) | C. | [$\frac{9}{10}$,1) | D. | [$\frac{5}{7}$,1] |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com