
設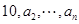 是各項均不為零的
是各項均不為零的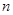 (
(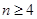 )項等差數列,且公差
)項等差數列,且公差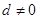 .
.
(1)若 ,且該數列前
,且該數列前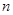 項和
項和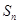 最大,求
最大,求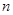 的值;
的值;
(2)若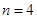 ,且將此數列刪去某一項后得到的數列(按原來的順序)是等比數列,求
,且將此數列刪去某一項后得到的數列(按原來的順序)是等比數列,求 的值;
的值;
(3)若該數列中有一項是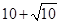 ,則數列
,則數列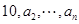 中是否存在不同三項(按原來的順序)為等比數列?請說明理由.
中是否存在不同三項(按原來的順序)為等比數列?請說明理由.
(1)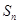 取最大時
取最大時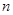 的值為30或31;(2)
的值為30或31;(2) 的值為
的值為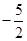 或10
或10
解析試題分析:(1)由等差數列前n項和的二次函數性質求解
(2)分類討論思想,依次分刪去第一項、第二項、第三項、第四項后成等比數列求解;
(3)考慮反證法
試題解析:(1)解法一:由已知得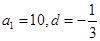
∴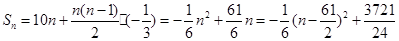
∵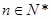 ∴
∴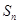 取最大時
取最大時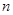 的值為30或31.
的值為30或31.
解法二:由已知得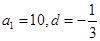 ∴
∴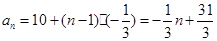 .
.
若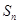 取最大,則只需
取最大,則只需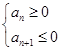 即
即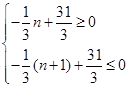 解得
解得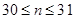 .
.
∵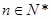 ∴當
∴當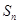 取最大時
取最大時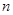 的值分別是30或31.
的值分別是30或31.
(2)當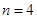 時,該數列的前4項可設為10、
時,該數列的前4項可設為10、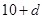 、
、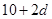 、
、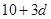 .
.
若刪去第一項10,則由題意得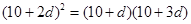 ,解得
,解得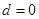 ,不符合題意.
,不符合題意.
若刪去第二項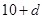 ,則由題意得
,則由題意得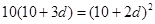 解得
解得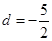 ,符合題意.
,符合題意.
若刪去第三項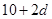 ,則由題意得
,則由題意得 解得
解得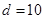 ,符合題意.
,符合題意.
若刪去第四項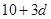 ,則由題意得
,則由題意得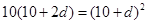 解得
解得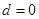 ,不符合題意.
,不符合題意.
綜上所述, 的值為
的值為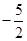 或10.
或10.
(3)設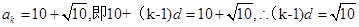
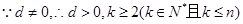
設該數列存在不同的三項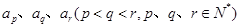 成等比數列,則
成等比數列,則 ,化簡得
,化簡得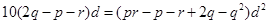
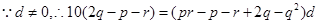
又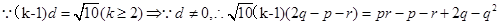
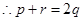 將
將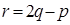 代入
代入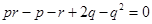 得
得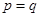 這與題設
這與題設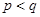 矛盾
矛盾
故該數列不存在不同三項(按原來的順序)為等比數列.
考點:等差數列的定義及性質,等比數列的定義及性質


科目:高中數學 來源: 題型:解答題
已知等差數列{ }的首項為
}的首項為 a
a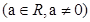 .設數列的前n項和為Sn,且對任意正整數n都有
.設數列的前n項和為Sn,且對任意正整數n都有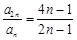 .
.
(1)求數列{ }的通項公式及Sn;
}的通項公式及Sn;
(2)是否存在正整數n和k,使得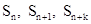 成等比數列?若存在,求出n和k的值;若不存在,請說明理由.
成等比數列?若存在,求出n和k的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列的前n項和為Sn,并且滿足a1=2,nan+1=Sn+n(n+1).
(1)求{an}的通項公式;
(2)令Tn=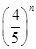 Sn,是否存在正整數m,對一切正整數n,總有Tn≤Tm?若存在,求m的值;若不存在,說明理由.
Sn,是否存在正整數m,對一切正整數n,總有Tn≤Tm?若存在,求m的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com