【題目】已知向量 
=（2cosωx，cos2ωx）， 
=（sinωx，1）（其中ω＞0），令f（x）= 
，且f（x）的最小正周期為π．
（1）求 
的值；
（2）寫出 
上的單調遞增區間．
【答案】
（1）解：f（x）= 
=2cosωxsinωx+cos2ωx
=sin2ωx+cos2ωx
= 
．
∵f（x）的最小正周期為π，∴ω=1．
∴ 
．
∴ 
（2）解：∵ ，
∴當﹣ 
，
即﹣ 
（k∈Z）時，f（x）單調遞增，
∵ 
，
∴f（x）在 
上的單調遞增區間為 
．
【解析】（1）把向量 
=（2cosωx，cos2ωx）， 
=（sinωx，1）代入f（x）= ，利用二倍角公式和兩角和的正弦函數化為： ，根據周期求出ω，然后求解 
的值；（2）利用正弦函數的單調增區間求出函數f（x）的單調增區間，選擇適當的k值求出 
上的單調遞增區間
【考點精析】利用正弦函數的單調性對題目進行判斷即可得到答案，需要熟知正弦函數的單調性：在
上是增函數；在
上是減函數．
科目：高中數學 來源： 題型：
【題目】某家電公司銷售部門共有200位銷售員，每位部門對每位銷售員都有1400萬元的年度銷售任務，已知這200位銷售員去年完成銷售額都在區間
（單位：百萬元）內，現將其分成5組，第1組，第2組，第3組，第4組，第5組對應的區間分別為
， 
， 
， 
， 
，繪制出頻率分布直方圖.
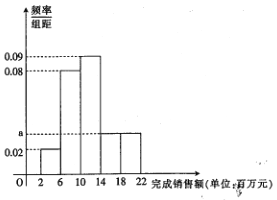
（1）求
的值，并計算完成年度任務的人數；
（2）用分層抽樣從這200位銷售員中抽取容量為25的樣本，求這5組分別應抽取的人數；
（3）現從（2）中完成年度任務的銷售員中隨機選取2位，獎勵海南三亞三日游，求獲得此獎勵的2位銷售員在同一組的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知 
=（cosx，﹣ 
）， 
=（sinx+cosx，1），f（x）= ，
（1）若0＜α＜ 
，sinα= 
，求f（α）的值；
（2）求函數f（x）的最小正周期及單調遞增區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π），在同一周期內，當x= 
時，f（x）取得最大值3；當x= 
時，f（x）取得最小值﹣3．
（1）求函數f（x）的解析式；
（2）求函數f（x）的單調遞減區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某同學用“隨機模擬方法”計算曲線
與直線
， 
所圍成的曲邊三角形的面積時，用計算機分別產生了10個在區間
上的均勻隨機數
和10個區間
上的均勻隨機數
（
， 
），其數據如下表的前兩行.
| 2.50 | 1.01 | 1.90 | 1.22 | 2.52 | 2.17 | 1.89 | 1.96 | 1.36 | 2.22 |
| 0.84 | 0.25 | 0.98 | 0.15 | 0.01 | 0.60 | 0.59 | 0.88 | 0.84 | 0.10 |
| 0.90 | 0.01 | 0.64 | 0.20 | 0.92 | 0.77 | 0.64 | 0.67 | 0.31 | 0.80 |
由此可得這個曲邊三角形面積的一個近似值是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
