
【題目】袋中共有8個乒乓球,其中有5個白球,3個紅球,這些乒乓球除顏色外完全相同.從袋中隨機取出一球,如果取出紅球,則把它放回袋中;如果取出白球,則該白球不再放回,并且另補一個紅球放入袋中,重復上述過程![]() 次后,袋中紅球的個數記為
次后,袋中紅球的個數記為![]() .
.
(I)求隨機變量![]() 的概率分布及數學期望
的概率分布及數學期望![]() ;
;
(Ⅱ)求隨機變量![]() 的數學期望
的數學期望![]() 關于
關于![]() 的表達式.
的表達式.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,曲線
軸正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]()
![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)已知點![]() ,若點
,若點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 經過點
經過點![]() 且與曲線
且與曲線![]() 相交于
相交于![]() 兩點,設線段
兩點,設線段![]() 的中點為
的中點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代名詞“芻童”原來是草堆的意思,古代用它作為長方體棱臺(上、下底面均為矩形額棱臺)的專用術語,關于“芻童”體積計算的描述,《九章算術》注曰:“倍上表,下表從之,亦倍小表,上表從之,各以其廣乘之,并,以高若深乘之,皆六面一.”其計算方法是:將上底面的長乘二,與下底面的長相加,再與上底面的寬相乘;將下底面的長乘二,與上底面的長相加,再與下底面的寬相乘;把這兩個數值相加,與高相乘,再取其六分之一,以此算法,現有上下底面為相似矩形的棱臺,相似比為![]() ,高為3,且上底面的周長為6,則該棱臺的體積的最大值是( )
,高為3,且上底面的周長為6,則該棱臺的體積的最大值是( )
A. 14 B. 56 C. ![]() D. 63
D. 63
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標平面內,以坐標原點![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.已知曲線
軸的非負半軸為極軸建立極坐標系.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,直線
,直線![]() 的參數方程為
的參數方程為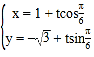 (
(![]() 為參數).
為參數).
(1)分別求出曲線![]() 和直線
和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 在曲線
在曲線![]() 上,且
上,且![]() 到直線
到直線![]() 的距離為1,求滿足這樣條件的點
的距離為1,求滿足這樣條件的點![]() 的個數.
的個數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的中心在原點,離心率等于
的中心在原點,離心率等于![]() ,它的一個短軸端點恰好是拋物線
,它的一個短軸端點恰好是拋物線![]() 的焦點.
的焦點.
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 、
、![]() 是橢圓上的兩點,
是橢圓上的兩點,![]() 是橢圓上位于直線
是橢圓上位于直線![]() 兩側的動點.
兩側的動點.
①若直線![]() 的斜率為
的斜率為![]() ,求四邊形
,求四邊形![]() 面積的最大值;
面積的最大值;
②當![]() 運動時,滿足
運動時,滿足![]() ,試問直線
,試問直線![]() 的斜率是否為定值,請說明理由.
的斜率是否為定值,請說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2+bx+c(a>0),且f(1)![]() .
.
(1)求證:函數f(x)有兩個不同的零點;
(2)設x1,x2是函數f(x)的兩個不同的零點,求|x1﹣x2|的取值范圍;
(3)求證:函數f(x)在區間(0,2)內至少有一個零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l1:kx-y+4=0與直線l2:x+ky-3=0相交于點P,則當實數k變化時,點P到直線4x-3y+10=0的距離的最大值為( )
A.2B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() .
.
(1)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(2)若函數![]() ,求
,求![]() 的單調區間;并證明:當
的單調區間;并證明:當![]() 時,
時,![]() ;
;
(3)證明:當![]() 時,函數
時,函數 有最小值,設
有最小值,設![]() 最小值為
最小值為![]() ,求函數
,求函數![]() 的值域.
的值域.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com