
【題目】已知拋物線C的頂點為坐標(biāo)原點O,對稱軸為x軸,其準(zhǔn)線過點![]() .
.
(1)求拋物線C的方程;
(2)過拋物線焦點F作直線l,使得拋物線C上恰有三個點到直線l的距離都為![]() ,求直線l的方程.
,求直線l的方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由題意得,拋物線的焦點在![]() 軸上,設(shè)拋物線C的方程為
軸上,設(shè)拋物線C的方程為![]() ,由準(zhǔn)線過點
,由準(zhǔn)線過點![]() ,可得
,可得![]() ,從而求解.
,從而求解.
(2)求出拋物線C的焦點為![]() ,分類討論直線l的斜率不存在時,驗證不合題意;當(dāng)直線l的斜率存在時,設(shè)直線l的方程為
,分類討論直線l的斜率不存在時,驗證不合題意;當(dāng)直線l的斜率存在時,設(shè)直線l的方程為![]() ,要滿足題意,需使在含坐標(biāo)原點的弧上有且只有一個點P到直線l的距離為
,要滿足題意,需使在含坐標(biāo)原點的弧上有且只有一個點P到直線l的距離為![]() ,過點P的直線平行直線
,過點P的直線平行直線![]() 且與拋物線C相切,設(shè)該切線方程為
且與拋物線C相切,設(shè)該切線方程為![]() ,代入拋物線方程,使判別式等于零,再利用兩平行線間的距離公式即可求解.
,代入拋物線方程,使判別式等于零,再利用兩平行線間的距離公式即可求解.
(1)由題意得,拋物線的焦點在![]() 軸正半軸上,設(shè)拋物線C的方程為
軸正半軸上,設(shè)拋物線C的方程為![]() ,
,
因為準(zhǔn)線過點![]() ,所以
,所以![]() ,即
,即![]() .
.
所以拋物線C的方程為![]() .
.
(2)由題意可知,拋物線C的焦點為![]() .
.
當(dāng)直線l的斜率不存在時,C上僅有兩個點到l的距離為![]() ,不合題意;
,不合題意;
當(dāng)直線l的斜率存在時,設(shè)直線l的方程為![]() ,
,
要滿足題意,需使在含坐標(biāo)原點的弧上有且只有一個點P到直線l的距離為![]() ,
,
過點P的直線平行直線![]() 且與拋物線C相切.
且與拋物線C相切.
設(shè)該切線方程為![]() ,
,
代入![]() ,可得
,可得![]() .
.
由![]() ,得
,得![]() .
.
由![]() ,整理得
,整理得![]() ,
,
又![]() ,解得
,解得![]() ,即
,即![]() .
.
因此,直線l方程為![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)統(tǒng)計,某蔬菜基地西紅柿畝產(chǎn)量的增加量![]() (百千克)與某種液體肥料每畝使用量
(百千克)與某種液體肥料每畝使用量![]() (千克)之間的對應(yīng)數(shù)據(jù)的散點圖,如圖所示.
(千克)之間的對應(yīng)數(shù)據(jù)的散點圖,如圖所示.
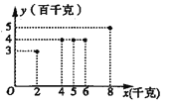
(1)依據(jù)數(shù)據(jù)的散點圖可以看出,可用線性回歸模型擬合![]() 與
與![]() 的關(guān)系,請計算相關(guān)系數(shù)
的關(guān)系,請計算相關(guān)系數(shù)![]() 并加以說明(若
并加以說明(若![]() ,則線性相關(guān)程度很高,可用線性回歸模型擬合);
,則線性相關(guān)程度很高,可用線性回歸模型擬合);
(2)求![]() 關(guān)于
關(guān)于![]() 的回歸方程,并預(yù)測液體肥料每畝使用量為12千克時,西紅柿畝產(chǎn)量的增加量
的回歸方程,并預(yù)測液體肥料每畝使用量為12千克時,西紅柿畝產(chǎn)量的增加量![]() 約為多少?
約為多少?
附:相關(guān)系數(shù)公式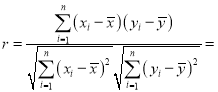
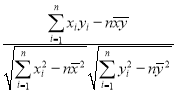 ,參考數(shù)據(jù):
,參考數(shù)據(jù):![]() ,
,![]() .
.
回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為: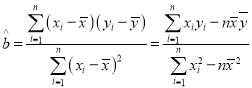 ,
,![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某班共有![]() 名學(xué)生,已知以下信息:
名學(xué)生,已知以下信息:
①男生共有![]() 人;
人;
②女團員共有![]() 人;
人;
③住校的女生共有![]() 人;
人;
④不住校的團員共有![]() 人;
人;
⑤住校的男團員共有![]() 人;
人;
⑥男生中非團員且不住校的共有![]() 人;
人;
⑦女生中非團員且不住校的共有![]() 人.
人.
根據(jù)以上信息,該班住校生共有______人![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義在![]() 上的奇函數(shù)
上的奇函數(shù)![]() 有最小正周期4,且
有最小正周期4,且![]() 時,
時,![]()
(1)判斷并證明![]() 在
在![]() 上的單調(diào)性,并求
上的單調(diào)性,并求![]() 在
在![]() 上的解析式;
上的解析式;
(2)當(dāng)![]() 為何值時,關(guān)于
為何值時,關(guān)于![]() 的方程
的方程![]() 在
在![]() 上有實數(shù)解?
上有實數(shù)解?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為更好地落實農(nóng)民工工資保證金制度,南方某市勞動保障部門調(diào)查了![]() 年下半年該市
年下半年該市![]() 名農(nóng)民工(其中技術(shù)工、非技術(shù)工各
名農(nóng)民工(其中技術(shù)工、非技術(shù)工各![]() 名)的月工資,得到這
名)的月工資,得到這![]() 名農(nóng)民工月工資的中位數(shù)為
名農(nóng)民工月工資的中位數(shù)為![]() 百元(假設(shè)這
百元(假設(shè)這![]() 名農(nóng)民工的月工資均在
名農(nóng)民工的月工資均在![]() (百元)內(nèi))且月工資收入在
(百元)內(nèi))且月工資收入在![]() (百元)內(nèi)的人數(shù)為
(百元)內(nèi)的人數(shù)為![]() ,并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖:
,并根據(jù)調(diào)查結(jié)果畫出如圖所示的頻率分布直方圖:

(Ⅰ)求![]() ,
,![]() 的值;
的值;
(Ⅱ)已知這![]() 名農(nóng)民工中月工資高于平均數(shù)的技術(shù)工有
名農(nóng)民工中月工資高于平均數(shù)的技術(shù)工有![]() 名,非技術(shù)工有
名,非技術(shù)工有![]() 名,則能否在犯錯誤的概率不超過
名,則能否在犯錯誤的概率不超過![]() 的前提下認(rèn)為是不是技術(shù)工與月工資是否高于平均數(shù)有關(guān)系?
的前提下認(rèn)為是不是技術(shù)工與月工資是否高于平均數(shù)有關(guān)系?
參考公式及數(shù)據(jù): ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知圓![]() 經(jīng)過
經(jīng)過![]() 兩點,且圓心
兩點,且圓心![]() 在直線
在直線![]() 上.
上.

(1)求圓![]() 的方程;
的方程;
(2)已知過點![]() 的直線
的直線![]() 與圓
與圓![]() 相交截得的弦長為
相交截得的弦長為![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)已知點![]() ,在平面內(nèi)是否存在異于點
,在平面內(nèi)是否存在異于點![]() 的定點
的定點![]() ,對于圓
,對于圓![]() 上的任意動點
上的任意動點![]() ,都有
,都有![]() 為定值?若存在求出定點
為定值?若存在求出定點![]() 的坐標(biāo),若不存在說明理由.
的坐標(biāo),若不存在說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】定義全集![]() 的子集
的子集![]() 的特征函數(shù)
的特征函數(shù)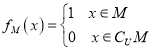 ,對于兩個集合
,對于兩個集合![]() ,定義集合
,定義集合![]() ,已知集合
,已知集合![]() ,并用
,并用![]() 表示有限集
表示有限集![]() 的元素個數(shù),則對于任意有限集
的元素個數(shù),則對于任意有限集![]() 的最小值為________.
的最小值為________.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com