
已知冪函數f(x)=x(m2+m)-1(m∈N*),經過點(2,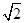 ),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
),試確定m的值,并求滿足條件f(2-a)>f(a-1)的實數a的取值范圍.
科目:高中數學 來源: 題型:解答題
設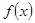 是定義在
是定義在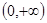 上的函數,且
上的函數,且 ,對任意
,對任意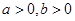 ,若經過點
,若經過點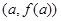 ,
,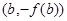 的直線與
的直線與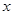 軸的交點為
軸的交點為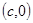 ,則稱
,則稱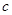 為
為 關于函數
關于函數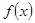 的平均數,記為
的平均數,記為 ,例如,當
,例如,當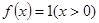 時,可得
時,可得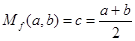 ,即
,即 為
為 的算術平均數.
的算術平均數.
當 時,
時, 為
為 的幾何平均數;
的幾何平均數;
當 時,
時, 為
為 的調和平均數
的調和平均數 ;
;
(以上兩空各只需寫出一個符合要求的函數即可)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設 (
(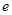 是自然對數的底數,
是自然對數的底數,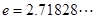 ),且
),且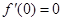 .
.
(1)求實數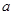 的值,并求函數
的值,并求函數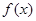 的單調區間;
的單調區間;
(2)設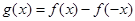 ,對任意
,對任意 ,恒有
,恒有 成立.求實數
成立.求實數 的取值范圍;
的取值范圍;
(3)若正實數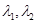 滿足
滿足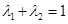 ,
,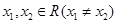 ,試證明:
,試證明: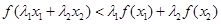 ;并進一步判斷:當正實數
;并進一步判斷:當正實數 滿足
滿足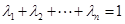
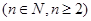 ,且
,且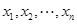 是互不相等的實數時,不等式
是互不相等的實數時,不等式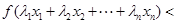
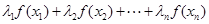 是否仍然成立.
是否仍然成立.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分14分)本題共有2個小題,第1小題滿分6分,第2個小題滿分8分。
某加油站擬造如圖所示的鐵皮儲油罐(不計厚度,長度單位:米),其中儲油罐的中間為圓柱形,左右兩端均為半球形,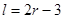 (
(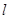 為圓柱的高,
為圓柱的高,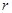 為球的半徑,
為球的半徑,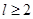 ).假設該儲油罐的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為
).假設該儲油罐的建造費用僅與其表面積有關.已知圓柱形部分每平方米建造費用為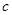 千元,半球形部分每平方米建造費用為3千元.設該儲油罐的建造費用為
千元,半球形部分每平方米建造費用為3千元.設該儲油罐的建造費用為 千元.
千元.
(1)寫出 關于
關于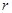 的函數表達式,并求該函數的定義域;
的函數表達式,并求該函數的定義域;
(2)求該儲油罐的建造費用最小時的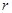 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某造紙廠擬建一座底面圖形為矩形且面積為162平方米的三級污水處理池,池的深度一定(平面圖如圖所示),如果池四周圍墻建造單價為400元/米,中間兩道隔墻建造單價為248元/米,池底建造單價為80元/平方米,水池所有墻的厚度忽略不計.
(1)試設計污水處理池的長和寬,使總造價最低,并求出最低總造價;
(2)若由于地形限制,該池的長和寬都不能超過16米,試設計污水處理池的長和寬,使總造價最低,并求出最低總造價.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
據市場分析,廣饒縣馳中集團某蔬菜加工點,當月產量在10噸至25噸時,月生產總成本 (萬元)可以看成月產量
(萬元)可以看成月產量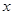 (噸)的二次函數.當月產量為10噸時,月總成本為20萬元;當月產量為15噸時,月總成本最低為17.5萬元.
(噸)的二次函數.當月產量為10噸時,月總成本為20萬元;當月產量為15噸時,月總成本最低為17.5萬元.
(1)寫出月總成本 (萬元)關于月產量
(萬元)關于月產量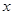 (噸)的函數關系;
(噸)的函數關系;
(2)已知該產品銷售價為每噸1.6萬元,那么月產量為多少時,可獲最大利潤;
(3)當月產量為多少噸時, 每噸平均成本最低,最低成本是多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com