
【題目】已知圓![]() 上一動點
上一動點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() .
.
(1)當![]() 在圓
在圓![]() 上運動時,求點
上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求線段
時,求線段![]() 的垂直平分線方程.
的垂直平分線方程.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】分析:(1)要求點![]() 的軌跡
的軌跡![]() 的方程,可設點
的方程,可設點![]() 的坐標為
的坐標為![]() ,由條件過點
,由條件過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() ,可寫出點A的坐標
,可寫出點A的坐標![]() 。因為點
。因為點![]() 在圓
在圓![]() 上,故可將點
上,故可將點![]() 的坐標代入圓
的坐標代入圓![]() 的方程
的方程![]() ,可得點
,可得點![]() 的軌跡
的軌跡![]() 。
。
(2)要線段![]() 的垂直平分線方程,應先求直線
的垂直平分線方程,應先求直線![]() 的方程,所以應設直線
的方程,所以應設直線![]() 的方程,根據弦長求直線
的方程,根據弦長求直線![]() 的方程。因為直線
的方程。因為直線![]() 的斜率是否存在不確定,為了避免討論,可設直線
的斜率是否存在不確定,為了避免討論,可設直線![]() 方程為:
方程為:![]() ,并與軌跡
,并與軌跡![]() 的方程聯立可得
的方程聯立可得![]() ,由根與系數的關系可得
,由根與系數的關系可得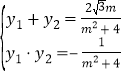 ,由弦長公式可得
,由弦長公式可得![]() ,可解得
,可解得![]() 。分情況討論,求線段
。分情況討論,求線段![]() 的中點,直線
的中點,直線![]() 的斜率,進而可求線段
的斜率,進而可求線段![]() 的垂直平分線方程。
的垂直平分線方程。
詳解:(1)設![]() ,則
,則![]()
將![]() 代入圓
代入圓![]() 方程得:點
方程得:點![]() 的軌跡
的軌跡![]()
(注:學生不寫![]() 也不扣分)
也不扣分)
(2)由題意可設直線![]() 方程為:
方程為:![]() ,
,
由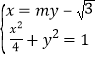 得:
得:![]()
所以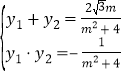
![]()
所以![]() .
.
當![]() 時,中點縱坐標
時,中點縱坐標![]() ,代入
,代入![]() 得:
得:
中點橫坐標![]() ,斜率為
,斜率為![]()
故![]() 的垂直平分線方程為:
的垂直平分線方程為:![]()
當![]() 時,同理可得
時,同理可得![]() 的垂直平分線方程為:
的垂直平分線方程為:![]()
所以![]() 的垂直平分線方程為:
的垂直平分線方程為:![]() 或
或![]() .
.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案科目:高中數學 來源: 題型:
【題目】某同學在研究函數f(x)=![]() (x∈R)時,分別給出下面幾個結論:
(x∈R)時,分別給出下面幾個結論:
①等式f(-x)=-f(x)在x∈R時恒成立;
②函數f(x)的值域為(-1,1);
③若x1≠x2,則一定有f(x1)≠f(x2);
④方程f(x)=x在R上有三個根.
其中正確結論的序號有______.(請將你認為正確的結論的序號都填上)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正方體![]() 中,若棱長為
中,若棱長為![]() ,點
,點![]() 分別為線段
分別為線段![]() 、
、![]() 上的動點,則下列結論正確結論的是( )
上的動點,則下列結論正確結論的是( )
A.![]() 面
面![]() B.面
B.面![]() 面
面![]()
C.點F到面![]() 的距離為定值
的距離為定值![]() D.直線
D.直線![]() 與面
與面![]() 所成角的正弦值為定值
所成角的正弦值為定值![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 上一動點
上一動點![]() ,過點
,過點![]() 作
作![]() 軸,垂足為
軸,垂足為![]() 點,
點,![]() 中點為
中點為![]() .
.
(1)當![]() 在圓
在圓![]() 上運動時,求點
上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線
的直線![]() 與
與![]() 交于
交于![]() 兩點,當
兩點,當![]() 時,求線段
時,求線段![]() 的垂直平分線方程.
的垂直平分線方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com