（08年潮州市二模理） 從6人中選出4人分別到巴黎、倫敦、香港、莫斯科四個城市游覽，要求每個城市有一人游覽，每人只能游覽一個城市，且這6人中甲、乙兩人不去巴黎游覽，則不同的選擇方案共有（ ）
A．
種 Ｂ．
種 Ｃ．
種 Ｄ．
種
暑假作業(yè)海燕出版社系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：高中數(shù)學(xué) 來源： 題型：
（08年潮州市二模理）（14分）已知函數(shù)
的導(dǎo)數(shù)
滿足
，常數(shù)
為方程
的實(shí)數(shù)根．
⑴ 若函數(shù)的定義域?yàn)镮，對任意
，存在
，使等式
=
成立，
求證：方程不存在異于的實(shí)數(shù)根；
⑵ 求證：當(dāng)
時，總有
成立；
⑶ 對任意
，若滿足
，求證
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
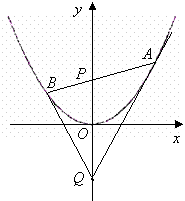
（08年潮州市二模理）（14分）如圖,過拋物線
的對稱軸上任一點(diǎn)
作直線與拋物線交于A、B兩點(diǎn)，點(diǎn)Q是點(diǎn)P關(guān)于原點(diǎn)的對稱點(diǎn)．
⑴ 設(shè)點(diǎn)P滿足
（
為實(shí)數(shù)），證明：
；
⑵ 設(shè)直線AB的方程是
，過A、B兩點(diǎn)的圓C與拋物線在點(diǎn)A處有共同的切線，求圓C的方程．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
（08年潮州市二模理）（14分）
如圖，四面體ABCD中，O、E分別是BD、BC的中點(diǎn)， 
⑴ 求證：
平面BCD；
⑵ 求異面直線AB與CD所成角余弦的大小；
⑶ 求點(diǎn)E到平面ACD的距離．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
（08年潮州市二模理）（14分）已知等差數(shù)列
的前項(xiàng)和為
，
，且
，
．
⑴．求數(shù)列
的通項(xiàng)公式；
⑵．求證：
．
查看答案和解析>>
科目：高中數(shù)學(xué) 來源： 題型：
（08年潮州市二模理） 我們知道：“過圓為
的圓外一點(diǎn)
作它的兩條切線
、
，其中
、
為切點(diǎn)，則
．”這個性質(zhì)可以推廣到所有圓錐曲線，請你寫出其中一個：
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com