
【題目】如果對一切正實數![]() ,
,![]() ,不等式
,不等式![]() 恒成立,則實數
恒成立,則實數![]() 的取值范圍是( )
的取值范圍是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
將不等式![]() cos2x≥asinx
cos2x≥asinx![]() 恒成立轉化為
恒成立轉化為![]() asinx+1﹣sin2x恒成立,構造函數f(y)
asinx+1﹣sin2x恒成立,構造函數f(y)![]() ,利用基本不等式可求得f(y)min=3,于是問題轉化為asinx﹣sin2x≤2恒成立.通過對sinx>0、sinx<0、sinx=0三類討論,可求得對應情況下的實數a的取值范圍,最后取其交集即可得到答案.
,利用基本不等式可求得f(y)min=3,于是問題轉化為asinx﹣sin2x≤2恒成立.通過對sinx>0、sinx<0、sinx=0三類討論,可求得對應情況下的實數a的取值范圍,最后取其交集即可得到答案.
解:實數x、y,不等式![]() cos2x≥asinx
cos2x≥asinx![]() 恒成立
恒成立![]() asinx+1﹣sin2x恒成立,
asinx+1﹣sin2x恒成立,
令f(y)![]() ,
,
則asinx+1﹣sin2x≤f(y)min,
∵y>0,f(y)![]() 2
2![]() 3(當且僅當y=6時取“=”),f(y)min=3;
3(當且僅當y=6時取“=”),f(y)min=3;
所以,asinx+1﹣sin2x≤3,即asinx﹣sin2x≤2恒成立.
①若sinx>0,a≤sinx![]() 恒成立,令sinx=t,則0<t≤1,再令g(t)=t
恒成立,令sinx=t,則0<t≤1,再令g(t)=t![]() (0<t≤1),則a≤g(t)min.
(0<t≤1),則a≤g(t)min.
由于g′(t)=1![]() 0,
0,
所以,g(t)=t![]() 在區間(0,1]上單調遞減,
在區間(0,1]上單調遞減,
因此,g(t)min=g(1)=3,
所以a≤3;
②若sinx<0,則a≥sinx![]() 恒成立,同理可得a≥﹣3;
恒成立,同理可得a≥﹣3;
③若sinx=0,0≤2恒成立,故a∈R;
綜合①②③,﹣3≤a≤3.
故選:D.


科目:高中數學 來源: 題型:
【題目】瑞士數學家、物理學家歐拉發現任一凸多面體(即多面體內任意兩點的連線都被完全包含在該多面體中,直觀上講是指沒有凹陷或孔洞的多面體)的頂點數V、棱數E及面數F滿足等式V﹣E+F=2,這個等式稱為歐拉多面體公式,被認為是數學領域最漂亮、簡潔的公式之一,現實生活中存在很多奇妙的幾何體,現代足球的外觀即取自一種不完全正多面體,它是由12塊黑色正五邊形面料和20塊白色正六邊形面料構成的.20世紀80年代,化學家們成功地以碳原子為頂點組成了該種結構,排列出全世界最小的一顆“足球”,稱為“巴克球(Buckyball)”.則“巴克球”的頂點個數為( )

A.180B.120C.60D.30
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為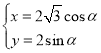 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,且
,且![]() 與
與![]() 交于
交于![]() ,
,![]() 兩點,已知點
兩點,已知點![]() 的極坐標為
的極坐標為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程,并求
的直角坐標方程,并求![]() 的值;
的值;
(2)若矩形![]() 內接于曲線
內接于曲線![]() 且四邊與坐標軸平行,求其周長的最大值.
且四邊與坐標軸平行,求其周長的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱錐![]() 中,底面
中,底面![]() 是邊長為6的正三角形,
是邊長為6的正三角形,![]() 底面
底面![]() ,且
,且![]() 與底面
與底面![]() 所成的角為
所成的角為![]() .
.
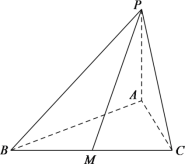
(1)求三棱錐![]() 的體積;
的體積;
(2)若![]() 是
是![]() 的中點,求異面直線
的中點,求異面直線![]() 與
與![]() 所成角的大小(結果用反三角函數值表示).
所成角的大小(結果用反三角函數值表示).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,若底面
中,若底面![]() 是正三角形,側棱長
是正三角形,側棱長![]() ,
,![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 的中點,并且
的中點,并且![]() ,則異面直線
,則異面直線![]() 與
與![]() 所成角為______;三棱錐
所成角為______;三棱錐![]() 的外接球的體積為______.
的外接球的體積為______.
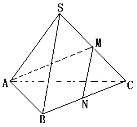
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示的幾何體中,正方形![]() 所在平面垂直于平面
所在平面垂直于平面![]() ,四邊形
,四邊形![]() 為平行四邊形,G為
為平行四邊形,G為![]() 上一點,且
上一點,且![]() 平面
平面![]() ,
,![]() .
.
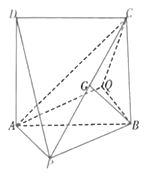
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當三棱錐![]() 體積最大時,求平面
體積最大時,求平面![]() 與平面
與平面![]() 所成二面角的正弦值.
所成二面角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 滿足
滿足![]() ,且
,且![]() ,
,![]() 分別是定義在
分別是定義在![]() 上的偶函數和奇函數.
上的偶函數和奇函數.
(1)求函數![]() 的反函數;
的反函數;
(2)已知![]() ,若函數
,若函數![]() 在
在![]() 上滿足
上滿足![]() ,求實數a的取值范圍;
,求實數a的取值范圍;
(3)若對于任意![]() 不等式
不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com