
在△ABC中,若 .
.
(Ⅰ)判斷△ABC的形狀;
(Ⅱ)在上述△ABC中,若角C的對邊 ,求該三角形內切圓半徑的取值范圍。
,求該三角形內切圓半徑的取值范圍。
(Ⅰ)直角三角形;(Ⅱ)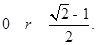
解析試題分析:(Ⅰ)先利用正弦定理和余弦定理把條件中關于角的等式轉化為關于邊的等式,再整理化簡,通過最終的等式可以判斷三角形的形狀.
(Ⅱ)利用(Ⅰ)的結果和切線的性質把內切圓的半徑用三角形的三條邊表示出來,再把三角邊轉化為角的形式,從而把問題轉化求三角函數的值域問題.
試題分析:(Ⅰ)根據正弦定理,原式可化為: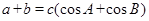 ,
,
再由余弦定理,上式可化為: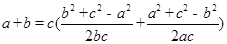 ,
,
即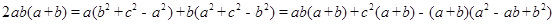
消去 整理得:
整理得: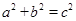 ,所以
,所以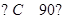 即△ABC為直角三角形.
即△ABC為直角三角形.
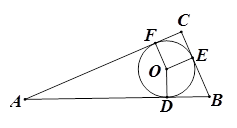
(Ⅱ)如圖,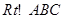 中,
中,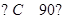 ,
,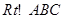 的內切圓
的內切圓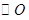 分別與邊
分別與邊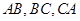 相切與點
相切與點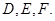
由切線長定理知: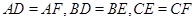
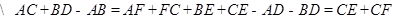
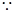 四邊形
四邊形 中,
中, 且
且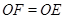
四邊形為正方形,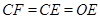
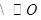 的半徑
的半徑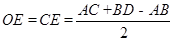
若設內切圓半徑為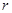 ,則
,則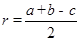 .
.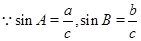 且
且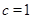 ,
,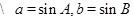 ,
,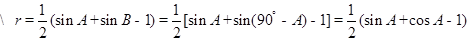
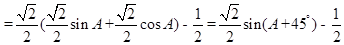
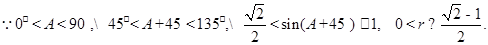
考點:1.正弦定理和余弦定理的應用;2.直角三角形內切圓的性質;3.三角恒等變換;4.三角函數的值域.


科目:高中數學 來源: 題型:解答題
已知向量 ,
, ,(
,( ,且
,且 為常數),設函數
為常數),設函數 ,若
,若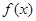 的最大值為1.
的最大值為1.
(1)求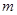 的值,并求
的值,并求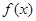 的單調遞增區間;
的單調遞增區間;
(2)在 中,角
中,角 、
、 、
、 的對邊
的對邊 、
、 、
、 ,若
,若 ,且
,且 ,試判斷三角形的形狀.
,試判斷三角形的形狀.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com