【題目】已知向量 
=（cos 
，sin ）， 
=（cos 
，﹣sin ），且x∈[ 
，π]．
（1）求 及| + |；
（2）求函數f（x）= +| + |的最大值，并求使函數取得最大值時x的值．
小學數學口算題卡脫口而出系列答案
優秀生應用題卡口算天天練系列答案
浙江之星課時優化作業系列答案科目：高中數學 來源： 題型：
【題目】如圖所示，已知點A（1，0），D（﹣1，0），點B，C在單位圓O上，且∠BOC= 
． 
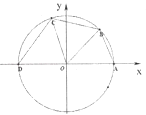
（Ⅰ）若點B（ 
， 
），求cos∠AOC的值；
（Ⅱ）設∠AOB=x（0＜x＜ 
），四邊形ABCD的周長為y，將y表示成x的函數，并求出y的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是等差數列，若a9+3a11＜0，a10a11＜0，且數列{an}的前n項和Sn有最大值，那么Sn取得最小正值時n等于（ ）
A.20
B.17
C.19
D.21
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
， 
， 
．
（1）討論函數
的單調性；
（2）記
，設
， 
為函數
圖象上的兩點，且
．
（ⅰ）當
， 
時，若
在
處的切線相互垂直，求證： 
；
（ⅱ）若
在點
處的切線重合，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
已知直線
的參數方程為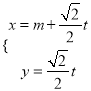
（
為參數），以坐標原點
為極點，以
軸正半軸為極軸，建立極坐標系，曲線
的極坐標方程為
，且曲線
的左焦點
在直線上．
（1）若直線
與曲線
交于
兩點，求
的值；
（2）設曲線
的內接矩形的周長為
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知遞增等比數列{an}的第三項、第五項、第七項的積為512，且這三項 分別減去1，3，9后成等差數列．
（1）求{an}的首項和公比；
（2）設Sn=a12+a22+…+an2 ， 求Sn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】用an表示自然數n的所有因數中最大的那個奇數，例如：9的因數有1，3，9，則a9=9；10的因數有1，2，5，10，則a10=5，記數列{an}的前n項和為Sn ， 則S 
= ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知方程C：x2+y2﹣2x﹣4y+m=0，
（1）若方程C表示圓，求實數m的范圍；
（2）在方程表示圓時，該圓與直線l：x+2y﹣4=0相交于M、N兩點，且|MN|= 
，求m的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
