
【題目】如圖,F1 , F2分別是橢圓C: ![]() =1(a>b>0)的左、右焦點,且焦距為2
=1(a>b>0)的左、右焦點,且焦距為2 ![]() ,動弦AB平行于x軸,且|F1A|+|F1B|=4.
,動弦AB平行于x軸,且|F1A|+|F1B|=4.
(1)求橢圓C的方程;
(2)若點P是橢圓C上異于點 ![]() 、A,B的任意一點,且直線PA、PB分別與y軸交于點M、N,若MF2、NF2的斜率分別為k1、k2 , 求證:k1k2是定值.
、A,B的任意一點,且直線PA、PB分別與y軸交于點M、N,若MF2、NF2的斜率分別為k1、k2 , 求證:k1k2是定值.
【答案】
(1)
解:∵焦距2 ![]() ,∴2c=2
,∴2c=2 ![]() ,得c=
,得c= ![]() ,
,
由橢圓的對稱性及已知得|F1A|=|F2B|,又∵|F1A|+|F1B|=4,|F1B|+|F2B|=4,
因此2a=4,a=2,于是b= ![]() ,因此橢圓方程為
,因此橢圓方程為 ![]()
(2)
解:設B(x0,y0),P(x1,y1),則A(﹣x0,y0),
直線PA的方程為 ![]() ,令x=0,得
,令x=0,得 ![]() ,
,
故M(0, ![]() );
);
直線PB的方程為 ![]() ,令x=0,得
,令x=0,得 ![]() ,
,
故N(0, ![]() );
);
∴ ![]() ,
, ![]() ,
,
因此 ![]() .
.
∵A,B在橢圓C上,∴ ![]() ,
,
∴ 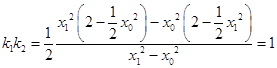
【解析】(1)由題意焦距求得c,由對稱性結合|F1A|+|F1B|=4可得2a,再由隱含條件求得b,則橢圓方程可求;(2)設B(x0 , y0),P(x1 , y1),則A(﹣x0 , y0),分別寫出PA、PB所在直線方程,求出M、N的坐標,進一步求出MF2、NF2的斜率分別為k1、k2 , 結合A、B在橢圓上可得k1k2是定值.


 天天向上課時同步訓練系列答案
天天向上課時同步訓練系列答案 陽光課堂同步練習系列答案
陽光課堂同步練習系列答案科目:高中數學 來源: 題型:
【題目】已知 ![]() 是定義在
是定義在 ![]() 上的可導函數
上的可導函數 ![]() 的導數,對任意
的導數,對任意 ![]()
![]() ,且
,且 ![]() ,且
,且 ![]() ,都有
,都有 ![]() ,
, ![]() ,
, ![]() ,則下列結論錯誤的是( )
,則下列結論錯誤的是( )
A.![]() 的增區間為
的增區間為 ![]()
B.![]() 在
在 ![]() =3處取極小值,在
=3處取極小值,在 ![]() =-1處取極大值??
=-1處取極大值??
C.![]() 有3個零點
有3個零點
D.![]() 無最大值也無最小值
無最大值也無最小值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}各項為正數,且a2=4a1 , an+1= ![]() +2an(n∈N*)
+2an(n∈N*)
(I)證明:數列{log3(1+an)}為等比數列;
(Ⅱ)令bn=log3(1+a2n﹣1),數列{bn}的前n項和為Tn , 求使Tn>345成立時n的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足a1=1,a2=3,若|an+1﹣an|=2n(n∈N*),且{a2n﹣1}是遞增數列、{a2n}是遞減數列,則 ![]()
![]() = .
= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合M={(x,y)|y=f(x)},若對于任意實數對(x1 , y1)∈M,存在(x2 , y2)∈M,使x1x2+y1y2=0成立,則稱集合M是“垂直對點集”.給出下列四個集合: ①M={(x,y)|y= ![]() };
};
②M={(x,y)|y=log2x};
③M={(x,y)|y=2x﹣2};
④M={(x,y)|y=sinx+1}.
其中是“垂直對點集”的序號是( )
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設雙曲線C: ![]() ,F1 , F2為其左右兩個焦點.
,F1 , F2為其左右兩個焦點.
(1)設O為坐標原點,M為雙曲線C右支上任意一點,求 ![]() 的取值范圍;
的取值范圍;
(2)若動點P與雙曲線C的兩個焦點F1 , F2的距離之和為定值,且cos∠F1PF2的最小值為 ![]() ,求動點P的軌跡方程.
,求動點P的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD與
平面ABCD所成的角依次是 ![]() 和
和 ![]() ,AP=2,E、F依次是PB、PC的中點;
,AP=2,E、F依次是PB、PC的中點;
(1)求異面直線EC與PD所成角的大小;(結果用反三角函數值表示)
(2)求三棱錐P﹣AFD的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點F1、F2為雙曲線C:x2﹣ ![]() =1的左、右焦點,過F2作垂直于x軸的直線,在x軸上方交雙曲線C于點M,∠MF1F2=30°.
=1的左、右焦點,過F2作垂直于x軸的直線,在x軸上方交雙曲線C于點M,∠MF1F2=30°.
(1)求雙曲線C的方程;
(2)過雙曲線C上任意一點P作該雙曲線兩條漸近線的垂線,垂足分別為P1、P2 , 求 ![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知a>0,b∈R,函數f(x)=4ax2﹣2bx﹣a+b的定義域為[0,1].
(1)當a=1時,函數f(x)在定義域內有兩個不同的零點,求b的取值范圍;
(2)設f(x)的最大值和最小值分別為M和m,求證:M+m>0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com