Question

已知數列{a_n}的前n項和為S_n，且S_n=-n²+20n，n∈N^*．
（Ⅰ）求通項a_n；
（Ⅱ）設{b_n-a_n}是首項為1，公比為3的等比數列，求數列{b_n}的通項公式及其前n項和T_n．

Answer 1

【答案】分析：（I）當n=1時，a₁=S₁=19；當n≥2時，a_n=S_n-S_n-1即可得出；
（II）利用等比數列的定義及其前n項和公式即可得出．
解答：解：（I）當n=1時，a₁=S₁=19；
當n≥2時，a_n=S_n-S_n-1=-n²+20n-[-（n-1）²+20（n-1）]=-2n+21，當n=1時也成立．
綜上可知：．
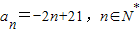
（II）∵{b_n-a_n}是首項為1，公比為3的等比數列，
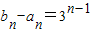
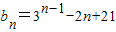
∴，∴（n∈N^*）．
∴
=
=．
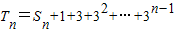
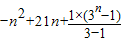
點評：熟練掌握\等比數列的定義及其前n項和公式是解題的關鍵．