
【題目】已知函數![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 在
在![]() 上的單調區間;
上的單調區間;
(3)求![]() 在
在![]() 上的最大值.
上的最大值.
【答案】(1)a=2,b=-4;(2)![]() 的增區間為
的增區間為 ![]() ;減區間為
;減區間為![]() ;(3)13.
;(3)13.
【解析】
(1)先對f(x)求導,把x=1代入導數式即可解出曲線在![]() 處的斜率k;把x=1代入原函數即可解出切點縱坐標,建立一個關于a和b的二元一次方程組,解方程可得a,b的值;
處的斜率k;把x=1代入原函數即可解出切點縱坐標,建立一個關于a和b的二元一次方程組,解方程可得a,b的值;
(2)求出f(x)的導數,由導數大于0,可得增區間;導數小于0,可得減區間;
(3)分別求出f(x)在區間[﹣3,1]上的極值和區間端點處的函數值,比較大小找出最大的值,即為函數在該閉區間上的最大值。
(1) 函數 ![]() 的導數為
的導數為 ![]() ,
,
曲線 ![]() 在點
在點 ![]() 處的切線斜率為
處的切線斜率為![]() ,
,
切點為![]() ,
,
由切線方程為 ![]() ,可得
,可得 ![]() ,
,![]() ,
,
解得![]() .
.
(2) 函數 ![]() 的導數
的導數![]() ,由
,由 ![]() ,可得
,可得 ![]() 或
或 ![]() ;由
;由 ![]() ,可得
,可得 ![]() .則 f(x) 的增區間為
.則 f(x) 的增區間為 ![]() ,
,![]() ;減區間為
;減區間為 ![]() .
.
(3) 由(2)可得 f(x) 的兩極值點-2,![]() ,
,
![]() ,
,![]() ,
,
又 ![]() ,
,![]() .
.
故 y=f(x) 在 ![]() 上的最大值為 13.
上的最大值為 13.


科目:高中數學 來源: 題型:
【題目】某電視傳媒公司為了了解某地區電視觀眾對某類體育節目的收視情況,隨機抽取了![]() 名觀眾進行調查,如圖是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖,將日均收看該體育節目時間不低于
名觀眾進行調查,如圖是根據調查結果繪制的觀眾日均收看該體育節目時間的頻率分布直方圖,將日均收看該體育節目時間不低于![]() 分鐘的觀眾稱為體育迷.
分鐘的觀眾稱為體育迷.
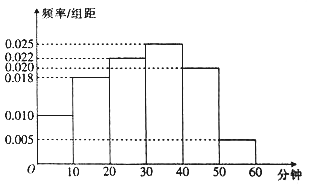
(1)以頻率為概率,若從這![]() 名觀眾中隨機抽取
名觀眾中隨機抽取![]() 名進行調查,求這
名進行調查,求這![]() 名觀眾中體育迷人數
名觀眾中體育迷人數![]() 的分布列;
的分布列;
(2)若抽取![]() 人中有女性
人中有女性![]() 人,其中女體育迷有
人,其中女體育迷有![]() 人,完成答題卡中的列聯表并判斷能否在犯錯概率不超過
人,完成答題卡中的列聯表并判斷能否在犯錯概率不超過![]() 的前提下認為是體育迷與性別有關系嗎?
的前提下認為是體育迷與性別有關系嗎?
附表及公式:
|
|
|
|
|
|
|
|
![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究機構對春節燃放煙花爆竹的天數x與霧霾天數y進行統計分析,得出下表數據.
x | 4 | 5 | 7 | 8 |
y | 2 | 3 | 5 | 6 |
(1)請根據上表提供的數據,用最小二乘法求出y關于x的線性回歸方程![]() ;
;
(2)試根據(1)求出的線性回歸方程,預測燃放煙花爆竹的天數為9的霧霾天數.
相關公式: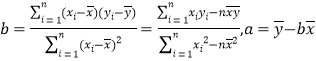
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=x2的圖象在點(x0 , x02)處的切線為l,若l也與函數y=lnx,x∈(0,1)的圖象相切,則x0必滿足( )
A.0<x0< ![]()
B.![]() <x0<1
<x0<1
C.![]() <x0<
<x0< ![]()
D.![]() <x0
<x0 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=logax(a>1)在[a,2a]上的最大值是最小值的2倍.
(1)若函數g(x)=f(3x2-mx+5)在區間[-1,+∞)上是增函數,求實數m的取值范圍;
(2)設函數F(x)=f(![]() )(2x),且關于x的方程F(x)=k在[
)(2x),且關于x的方程F(x)=k在[![]() ,4]上有解,求實數k的取值范圍.
,4]上有解,求實數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓的中心在原點,焦點在![]() 軸上,離心率為
軸上,離心率為![]() ,且經過點
,且經過點![]() ,直線
,直線![]() 交橢圓于不同的兩點
交橢圓于不同的兩點![]() .
.
(1)求橢圓的方程;
(2)求![]() 的取值范圍;
的取值范圍;
(3)若直線![]() 不過點
不過點![]() ,求證:直線
,求證:直線![]() 的斜率互為相反數.
的斜率互為相反數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在三棱柱ABC﹣A1B1C1中,側面AA1C1C⊥底面ABC,AA1=A1C=AC=AB=BC=2,且點O為AC中點. (Ⅰ)證明:A1O⊥平面ABC;
(Ⅱ)求二面角A﹣A1B﹣C1的大小.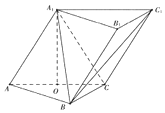
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若關于x的方程(x﹣1)4+mx﹣m﹣2=0各個實根x1 , x2…xk(k≤4,k∈N*)所對應的點(xi![]() ),(i=1,2,3…k)均在直線y=x的同側,則實數m的取值范圍是( )
),(i=1,2,3…k)均在直線y=x的同側,則實數m的取值范圍是( )
A.(﹣1,7)
B.(﹣∞,﹣7)U(﹣1,+∞)
C.(﹣7,1)
D.(﹣∞,1)U(7,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com