
【題目】已知函數y=x2的圖象在點(x0 , x02)處的切線為l,若l也與函數y=lnx,x∈(0,1)的圖象相切,則x0必滿足( )
A.0<x0< ![]()
B.![]() <x0<1
<x0<1
C.![]() <x0<
<x0< ![]()
D.![]() <x0
<x0 ![]()
【答案】D
【解析】解:函數y=x2的導數為y′=2x, 在點(x0 , x02)處的切線的斜率為k=2x0 ,
切線方程為y﹣x02=2x0(x﹣x0),
設切線與y=lnx相切的切點為(m,lnm),0<m<1,
即有y=lnx的導數為y′= ![]() ,
,
可得2x0= ![]() ,切線方程為y﹣lnm=
,切線方程為y﹣lnm= ![]() (x﹣m),
(x﹣m),
令x=0,可得y=lnm﹣1=﹣x02 ,
由0<m<1,可得x0> ![]() ,且x02>1,
,且x02>1,
解得x0>1,
由m= ![]() ,可得x02﹣ln(2x0)﹣1=0,
,可得x02﹣ln(2x0)﹣1=0,
令f(x)=x2﹣ln(2x)﹣1,x>1,
f′(x)=2x﹣ ![]() >0,f(x)在x>1遞增,
>0,f(x)在x>1遞增,
且f( ![]() )=2﹣ln2
)=2﹣ln2 ![]() ﹣1<0,f(
﹣1<0,f( ![]() )=3﹣ln2
)=3﹣ln2 ![]() ﹣1>0,
﹣1>0,
則有x02﹣ln(2x0)﹣1=0的根x0∈( ![]() ,
, ![]() ).
).
故選:D.
求出函數y=x2的導數,y=lnx的導數,求出切線的斜率,切線的方程,可得2x0= ![]() ,lnm﹣1=﹣x02 , 再由零點存在定理,即可得到所求范圍.
,lnm﹣1=﹣x02 , 再由零點存在定理,即可得到所求范圍.


科目:高中數學 來源: 題型:
【題目】某4S店開展汽車銷售業績比賽,現統計甲、乙兩名銷售員連續5個月的銷售業績(單位:臺)的莖葉圖如圖所示.
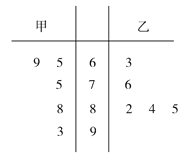
(1)作為業務主管的你認為誰的銷售情況好?請說明理由;
(2)若分別從甲、乙的銷售業績中任取一次,求兩人中至少有一人銷售業績在80臺以上的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知△ABC的內角A、B、C的對邊分別為a、b、c,且3bcos A=ccos A+acosC.
(1)求tanA的值;
(2)若a=4 ![]() ,求△ABC的面積的最大值.
,求△ABC的面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產企業研發了一種新產品,該產品在試銷一個階段后得到銷售單價![]() (單位:元)和銷售量
(單位:元)和銷售量![]() (單位:萬件)之間的一組數據,如下表所示:
(單位:萬件)之間的一組數據,如下表所示:
銷售單價 | 9 | 9.5 | 10 | 10.5 | 11 |
銷售量 | 11 | 10 | 8 | 6 | 5 |
(1)根據表中數據,建立![]() 關于的
關于的![]() 回歸方程;
回歸方程;
(2)從反饋的信息來看,消費者對該產品的心理價(單位:元/件)在![]() 內,已知該產品的成本是
內,已知該產品的成本是![]() 元/件(其中
元/件(其中![]() ),那么在消費者對該產品的心理價的范圍內,銷售單價定為多少時,企業才能獲得最大利潤?(注:利潤=銷售收入-成本)
),那么在消費者對該產品的心理價的范圍內,銷售單價定為多少時,企業才能獲得最大利潤?(注:利潤=銷售收入-成本)
參考數據:![]() ,
,![]() .
.
參考公式: ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com