
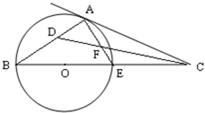
已知
AC切⊙O于C點,CP為⊙O直徑,AB切⊙O于D點,且與CP的延長線相交于B點,如圖,(1)若BD=2BP,求證:PC=3BP,AC=PC.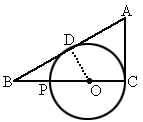
(2)
若PC=3BP,求證:BD=2BP,AC=PC.(3)
若AC=PC,求證:PC=3BP,BD=2BP.|
證明: (1)證法1:由切割線定理,得
連結 OD,如上圖,設⊙O半徑為r,∵ 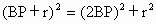 . .
∴ 由 △BDO∽△BCA得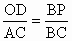 ,∴ ,∴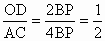 . .
∴AC=2DO=2r . ∴AC=PC.證法 2:如圖.
連結 DP和DC.∵∠BDP=∠C,∠B=∠B,∴△BPD∽△BDC .∴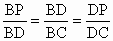 . .
∵BD=2BP ,∴BC=2BD=4BP.∴PC=3BP,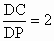 . .
再連結 OA,由切線長定理可得∵AD=AC ,AD平分∠BAC,∴OA⊥CD,∠ACB=90°.∵∠DCP=90 °-∠ACD=∠OAC,∠PDC=∠ACO=90°,∴△PDC∽△OCA .∴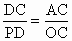 .∴AC=2OC=PC. .∴AC=2OC=PC.
還可如下證明: ∵ 易得DP∥AO,∴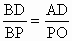 .
∵ .
∵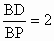 ,AD=AC, ,AD=AC,
∴AC=2PO=PC .(2) 由切割線定理,得∵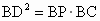 ,又∵PC=3BP, ,又∵PC=3BP,
∴BC=4BP ,∴BD=2BP.其他證法要與前面方法對照進行證明即可, (3) 如圖,易證DP∥AO,∴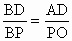 .又∵AD=AC,AC=PC, .又∵AD=AC,AC=PC,
∴ 又 ∵CM⊥AO,∠ACO=90°,由射線定理有 , ,
∵ 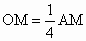 , ,
∵OC=OP ,CM=MD,∴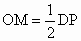 . .
∴ 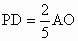 . .
∵AO∥DP ,∴△BPD∽△BOA.∴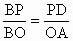 . .
∴ 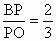 .∴3BP=2PO=PC. .∴3BP=2PO=PC.
此外其他證法仍可參照前面方法進行. |


科目:高中數(shù)學 來源: 題型:
 選修4-1:幾何證明選講
選修4-1:幾何證明選講查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
 請考生在第23,24,25題中任選一題作答,如果多做,則按所做的第一題計分,作答時請寫清題號.
請考生在第23,24,25題中任選一題作答,如果多做,則按所做的第一題計分,作答時請寫清題號.| AC | BC |
查看答案和解析>>
科目:高中數(shù)學 來源:2013屆吉林長春市高二第二次月考文科數(shù)學試卷(解析版) 題型:解答題
已知,如圖,AB是⊙O的直徑,AC切⊙O于點A,AC=AB,CO交⊙O于點P,CO的延長線交⊙O于點F, BP的延長線交AC于點E.
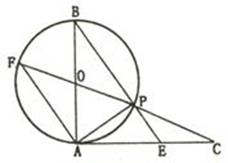
⑴求證:FA∥BE;
⑵求證: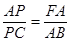
【解析】本試題主要是考查了平面幾何中圓與三角形的綜合運用。
(1)要證明線線平行,主要是通過證明線線平行的判定定理得到
(2)利用三角形△APC∽△FAC相似,來得到線段成比列的結論。
證明:(1)在⊙O中,∵直徑AB與FP交于點O ∴OA=OF
∴∠OAF=∠F ∵∠B=∠F ∴∠OAF=∠B ∴FA∥BE
(2)∵AC為⊙O的切線,PA是弦 ∴∠PAC=∠F
∵∠C=∠C ∴△APC∽△FAC ∴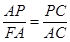
∴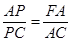 ∵AB=AC
∴
∵AB=AC
∴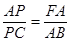
查看答案和解析>>
科目:高中數(shù)學 來源:2012屆河南鄭州市高二下學期第二次月考試題數(shù)學(文科) 題型:選擇題
如圖,已知AB是⊙O的弦,AC切⊙O于點A,∠BAC=60°,則∠ADB的度數(shù)為 ( )
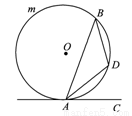
A. 60° B. 120°
C.140° D.150°
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com