
【題目】在函數(shù)定義域內(nèi),若存在區(qū)間![]() ,使得函數(shù)值域為
,使得函數(shù)值域為![]() ,則稱此函數(shù)為“
,則稱此函數(shù)為“![]() 檔類正方形函數(shù)”,已知函數(shù)
檔類正方形函數(shù)”,已知函數(shù)![]() .
.
(1)當(dāng)![]() 時,求函數(shù)
時,求函數(shù)![]() 的值域;
的值域;
(2)若函數(shù)![]() 的最大值是1,求實數(shù)
的最大值是1,求實數(shù)![]() 的值;
的值;
(3)當(dāng)![]() 時,是否存在
時,是否存在![]() ,使得函數(shù)
,使得函數(shù)![]() 為“1檔類正方形函數(shù)”?若存在,求出實數(shù)
為“1檔類正方形函數(shù)”?若存在,求出實數(shù)![]() 的取值范圍,若不存在,請說明理由.
的取值范圍,若不存在,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)根據(jù)指數(shù)函數(shù)的性質(zhì)和對數(shù)函數(shù)想性質(zhì)可得到函數(shù)![]() 的值域;
的值域;
(2)利用換元法設(shè)![]() ,然后對參數(shù)
,然后對參數(shù)![]() 進行分類討論,分
進行分類討論,分![]() 和
和![]() 兩種情況進行討論函數(shù)
兩種情況進行討論函數(shù)![]() 的最大值,根據(jù)最大值取得的情況計算出
的最大值,根據(jù)最大值取得的情況計算出![]() 的取值;
的取值;
(3)繼續(xù)利用換元法設(shè)![]() ,設(shè)真數(shù)為
,設(shè)真數(shù)為![]() ,根據(jù)二次函數(shù)的性質(zhì)可得
,根據(jù)二次函數(shù)的性質(zhì)可得![]() 在
在![]() 上為增函數(shù),則
上為增函數(shù),則![]() ,將問題轉(zhuǎn)化為方程
,將問題轉(zhuǎn)化為方程![]() 在
在![]() 上有兩個不同實根進行思考,再次利用換元法轉(zhuǎn)化為一元二次方程,根據(jù)
上有兩個不同實根進行思考,再次利用換元法轉(zhuǎn)化為一元二次方程,根據(jù)![]() ,及韋達定理可計算出實數(shù)
,及韋達定理可計算出實數(shù)![]() 的取值范圍.
的取值范圍.
(1)![]() 時,
時,![]() ,
,
因為![]() .
.
所以![]() ,
,
所以函數(shù)![]() 的值域為
的值域為![]()
(2)設(shè)![]() ,則
,則![]() ,
,
若![]() ,則函數(shù)
,則函數(shù)![]() 無最大值,
無最大值,
即![]() 無最大值,不合題意;
無最大值,不合題意;
故![]() ,因此
,因此![]() 最大值在
最大值在![]() 時取到,
時取到,
且![]() ,所以
,所以 ,
,
解得![]() 或
或![]() ,
,
由![]() ,所以
,所以![]() .
.
(3)因為![]() 時,設(shè)
時,設(shè)![]() .設(shè)真數(shù)為
.設(shè)真數(shù)為![]() .
.
此時對稱軸![]() ,
,
所以當(dāng)![]() 時,
時,![]() 為增函數(shù),且
為增函數(shù),且![]() ,
,
即![]() 在
在![]() 上為增函數(shù).
上為增函數(shù).
所以,![]() ,
,
即方程![]() 在
在![]() 上有兩個不同實根,
上有兩個不同實根,
即![]() ,設(shè)
,設(shè)![]() .
.
所以![]() .
.
即方程![]() 有兩個大于l的不等實根,
有兩個大于l的不等實根,
因為![]() ,
,
所以 ,
,
解得![]() ,
,
即存在![]() ,使得函數(shù)
,使得函數(shù)![]() 為“1檔類正方形函數(shù)”,且
為“1檔類正方形函數(shù)”,且![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖設(shè)計一幅矩形宣傳畫,要求畫面面積為4840![]() ,畫面上下邊要留8cm空白,左右要留5cm空白,怎樣確定畫面高與寬的尺寸,才能使宣傳畫所用紙張面積最小?
,畫面上下邊要留8cm空白,左右要留5cm空白,怎樣確定畫面高與寬的尺寸,才能使宣傳畫所用紙張面積最小?

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線![]() 和平面
和平面![]() :①若直線
:①若直線![]() 與平面
與平面![]() 內(nèi)的無數(shù)條直線平行,則
內(nèi)的無數(shù)條直線平行,則![]() ;②若直線
;②若直線![]() 與平面
與平面![]() 內(nèi)的任意一條直線都不平行,則直線
內(nèi)的任意一條直線都不平行,則直線![]() 和平面
和平面![]() 相交;③若
相交;③若![]() ,則直線
,則直線![]() 與平面
與平面![]() 內(nèi)某些直線平行;④若
內(nèi)某些直線平行;④若![]() ,則存在平面
,則存在平面![]() 內(nèi)的直線
內(nèi)的直線![]() ,使
,使![]() .以上結(jié)論中正確的個數(shù)為( )
.以上結(jié)論中正確的個數(shù)為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 在一個周期內(nèi)的圖象如圖所示.
在一個周期內(nèi)的圖象如圖所示.
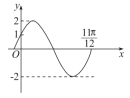
(1)求函數(shù)![]() 的解析式.
的解析式.
(2)求方程![]() 的解的個數(shù).
的解的個數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的空間幾何體中,平面![]() 平面
平面![]() ,
,![]() 與
與![]() 是邊長為2的等邊三角形,
是邊長為2的等邊三角形,![]() ,BE和平面ABC所成的角為
,BE和平面ABC所成的角為![]() ,且點E在平面ABC上的射影落在
,且點E在平面ABC上的射影落在![]() 的平分線上.
的平分線上.

(1)求證:![]() 平面ABC;
平面ABC;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(1)若![]() 個棱長為正整數(shù)的正方體的體積之和等于2005,求
個棱長為正整數(shù)的正方體的體積之和等于2005,求![]() 的最小值,并說明理由;
的最小值,并說明理由;
(2)若![]() 個棱長為正整數(shù)的正方體的體積之和等于
個棱長為正整數(shù)的正方體的體積之和等于![]() ,求
,求![]() 的最小值,并說明理由.
的最小值,并說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】由五個不同的數(shù)字0,1,2,5,![]() 組成無重復(fù)數(shù)字的三位數(shù)(最后結(jié)果用數(shù)字表達)
組成無重復(fù)數(shù)字的三位數(shù)(最后結(jié)果用數(shù)字表達)
(1)若![]() ,則組成的偶數(shù)有多少個?
,則組成的偶數(shù)有多少個?
(2)若![]() ,則比210大的數(shù)有多少個?
,則比210大的數(shù)有多少個?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某媒體為調(diào)查喜愛娛樂節(jié)目![]() 是否與觀眾性別有關(guān),隨機抽取了30名男性和30名女性觀眾,抽查結(jié)果用等高條形圖表示如圖:
是否與觀眾性別有關(guān),隨機抽取了30名男性和30名女性觀眾,抽查結(jié)果用等高條形圖表示如圖:
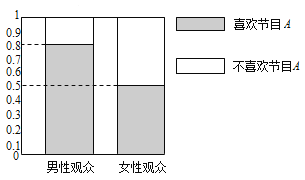
(1)根據(jù)該等高條形圖,完成下列![]() 列聯(lián)表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節(jié)目
列聯(lián)表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過0.05的前提下認為喜歡娛樂節(jié)目![]() 與觀眾性別有關(guān)?
與觀眾性別有關(guān)?

(2)從性觀眾中按喜歡節(jié)目![]() 與否,用分層抽樣的方法抽取5名做進一步調(diào)查.從這5名中任選2名,求恰有1名喜歡節(jié)目
與否,用分層抽樣的方法抽取5名做進一步調(diào)查.從這5名中任選2名,求恰有1名喜歡節(jié)目![]() 和1名不喜歡節(jié)目
和1名不喜歡節(jié)目![]() 的概率.
的概率.
附:
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
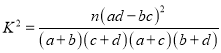 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]() .
.

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com