
【題目】袋中有7個球,其中4個白球,3個紅球,從袋中任意取出2個球,求下列事件的概率:
(1) ![]() 取出的2個球都是白球;
取出的2個球都是白球;
(2)![]() 取出的2個球中1個是白球,另1個是紅球.
取出的2個球中1個是白球,另1個是紅球.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)用列舉法可得從袋中7個球中一次任意取出2個球的基本事件的個數,其中取出的2個球均為白球的個數,再利用古典概型的概率計算公式即可得出;
(2)用列舉法得到取出的2個球中1個是白球,另1個是紅球基本事件個數,再利用古典概型的概率計算公式即可得.
設4個白球的編號為1,2,3,4,3個紅球的編號為5,6,7,從袋中的7個小球中任取2個的方法為(1,2),(1,3),(1,4),(1,5),(1,6),(1,7) ,(2,3),(2,4),(2,5),(2,6),(2,7) ,(3,4),(3,5),(3,6),(3,7) ,(4,5),(4,6),(4,7) ,(5,6), (5,7) ,(6,7) ,共21種.
(1)從袋中的7個球中任取2個,所取的2個球全是白球的方法總數,即是從4個白球中任取2個的方法總數,共有6種,即為(1,2),(1,3),(1,4),(2,3),(2,4),(3,4).∴取出的2個球全是白球的概率為![]()
(2)從袋中的7個球中任取2個,其中1個為紅球,而另1個為白球,其取法包括(1,5),(1,6),(1,7) ,(2,5),(2,6),(2,7) ,(3,5),(3,6),(3,7) ,(4,5),(4,6) ,(4,7) ,共12種.
∴取出的2個球中1個是白球,另1個是紅球的概率為![]() .
.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知點![]() 在橢圓
在橢圓![]() 上,將射線
上,將射線![]() 繞原點
繞原點![]() 逆時針旋轉
逆時針旋轉![]() ,所得射線
,所得射線![]() 交直線
交直線![]() 于點
于點![]() .以
.以![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系.
軸正半軸為極軸建立極坐標系.
(1)求橢圓![]() 和直線
和直線![]() 的極坐標方程;
的極坐標方程;
(2)證明::![]() 中,斜邊
中,斜邊![]() 上的高
上的高![]() 為定值,并求該定值.
為定值,并求該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】華中師大附中中科教處為了研究高一學生對物理和數學的學習是否與性別有關,從高一年級抽取60,名同學(男同學30名,女同學30名),給所有同學物理題和數學題各一題,讓每位同學自由選擇一道題進行解答.選題情況如下表:(單位:人)

(1)在犯錯誤的概率不超過1%是條件下,能否判斷高一學生對物理和數學的學習與性別有關?
(2)經過多次測試后發現,甲每次解答一道物理題所用的時間5—8分鐘,乙每次解答一道物理題所用的時間為6—8分鐘,現甲、乙解同一道物理題,求甲比乙先解答完的概率;
(3)現從選擇做物理題的8名女生中任意選取兩人,對題目的解答情況進行全程研究,記甲、乙兩女生被抽到的人數為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
,![]() ,過
,過![]() 且垂直于
且垂直于![]() 軸的焦點弦的弦長為
軸的焦點弦的弦長為![]() ,過
,過![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)已知直線![]() ,
,![]() 互相垂直,直線
互相垂直,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于點
交于點![]() ,
,![]() 兩點,直線
兩點,直線![]() 過
過![]() 且與橢圓
且與橢圓![]() 交于
交于![]() ,
,![]() 兩點.求
兩點.求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的極值;
的極值;
(Ⅱ)若函數![]() 的兩個零點為
的兩個零點為![]() ,記
,記![]() ,證明:
,證明:![]() .
.
【答案】(Ⅰ)極大值為![]() ,無極小值;(Ⅱ)證明見解析.
,無極小值;(Ⅱ)證明見解析.
【解析】分析:(Ⅰ)先判斷函數![]() 在
在![]() 上的單調性,然后可得當
上的單調性,然后可得當![]() 時,
時,![]() 有極大值,無極小值.(Ⅱ)不妨設
有極大值,無極小值.(Ⅱ)不妨設![]() ,由題意可得
,由題意可得![]() ,即
,即![]() ,又由條件得
,又由條件得![]() ,構造
,構造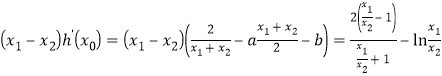 ,令
,令![]() ,則
,則![]() ,利用導數可得
,利用導數可得![]() ,故得
,故得![]() ,又
,又![]() ,所以
,所以![]() .
.
詳解:(Ⅰ)![]() ,
,
![]() ,
,
由![]() 得
得![]() ,
,
且當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() ,即
,即![]() 在
在![]() 上單調遞減,
上單調遞減,
∴當![]() 時,
時,![]() 有極大值,且
有極大值,且![]() ,無極小值.
,無極小值.
(Ⅱ)![]() 函數
函數![]() 的兩個零點為
的兩個零點為![]() ,不妨設
,不妨設![]() ,
,
![]() ,
,![]() .
.
![]()
![]() ,
,
即![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,

![]()
![]()
 .
.
令![]() ,則
,則![]()
![]() ,
,
![]() 在
在![]() 上單調遞減,
上單調遞減,
故![]() ,
,
 ,
,
即![]() ,
,
又![]() ,
,
![]() .
.
點睛:(1)研究方程根的情況,可以通過導數研究函數的單調性、最大(小)值、函數的變化趨勢等,根據題目要求,畫出函數圖象的大體圖象,然后通過數形結合的思想去分析問題,可以使得問題的求解有一個清晰、直觀的整體展現.
(2)證明不等式時常采取構造函數的方法,然后通過判斷函數的單調性,借助函數的最值進行證明.
【題型】解答題
【結束】
22
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ).以坐標原點
).以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,已知曲線
軸正半軸為極軸,建立極坐標系,已知曲線![]() 的極坐標方程為:
的極坐標方程為:![]() .
.
(Ⅰ)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設直線![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,若
,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com