【題目】已知 
， 
， 
是同一平面內的三個向量，其中 =（﹣ 
，1）．
（1）若| |=2 且 ∥ ，求 的坐標；
（2）若| |= ，（ +3 ）⊥（ ﹣ ），求向量 ， 的夾角的余弦值．
【答案】
（1）解：設 
=（m，n），
若| |=2 且 
∥ ，其中 =（﹣ 
，1），
可得m2+n2=4，m=﹣ n，
解得m=﹣ 
，n= 
或m= ，n=﹣ ，
則 =（﹣ ， ）或（ ，﹣ ）
（2）解：若 =（﹣ ，1），可得| |= 
，
又| 
|= ，（ +3 ）⊥（ ﹣ ），
可得（ +3 ）（ ﹣ ）= 2﹣3 2+2 =0，
即有3﹣3×2+2 =0，
可得 = 
，
向量 ， 的夾角的余弦值為 
= 
= 
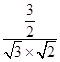【解析】（1）設 
=（m，n），運用向量模的公式和向量共線的坐標表示，解方程即可得到所求；（2）由向量垂直的條件：數量積為0，以及向量的平方即為模的平方，化簡整理，可得 
= 
，再由向量夾角的余弦公式，計算即可得到所求值．
科目：高中數學 來源： 題型：
【題目】已知F為拋物線y2=x的焦點，點A，B在該拋物線上且位于x軸的兩側， 
=2（其中O為坐標原點），則△ABO與△AFO面積之和的最小值是（ ）
A.2
B.3
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}是首項為正數的等差數列，a1a2=3，a2a3=15．
（1）求數列{an}的通項公式；
（2）設bn=（an+1）2 
，求數列{bn}的前n項和Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】由函數y=sin x 的圖象經過（ ）變換，得到函數 y=sin（2x﹣ 
）的圖象．
A.縱坐標不變，橫坐標縮小到原來的 
，再向右平移 個單位
B.縱坐標不變，向右平移 個單位，再橫坐標縮小到原來的
C.縱坐標不變，橫坐標擴大到原來的 2 倍，再向左平移 個單位
D.縱坐標不變，向左平移 個單位，再橫坐標擴大到原來的 2 倍
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】記所有非零向量構成的集合為V，對于 
， 
∈V， ≠ ，定義V（ ， ）=|x∈V|x =x |
（1）請你任意寫出兩個平面向量 ， ，并寫出集合V（ ， ）中的三個元素；
（2）請根據你在（1）中寫出的三個元素，猜想集合V（ ， ）中元素的關系，并試著給出證明；
（3）若V（ ， ）=V（ ， 
），其中 ≠ ，求證：一定存在實數λ1 ， λ2 ， 且λ1+λ2=1，使得 =λ1 +λ2 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若對于函數f（x）的定義域中任意的x1 ， x2（x1≠x2），恒有 
和 
成立，則稱函數f（x）為“單凸函數”，下列有四個函數：
（1）y=2x；（2）y=lgx；（3） 
；（4）y=x2 ．
其中是“單凸函數”的序號為 ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
（2x﹣2﹣x）（a＞0，且a≠1）．
（1）判斷函數f（x）的奇偶性和單調性，并說明理由；
（2）當x∈（﹣1，1）時，總有f（m﹣1）+f（m）＜0，求實數m的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
