
已知函數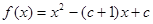
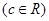 .
.
(1)解關于x的不等式f(x)<0;
(2)當c=-2時,不等式f(x)>ax-5在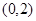 上恒成立,求實數a的取值范圍;
上恒成立,求實數a的取值范圍;
(1)當c<1時,不等式的解集為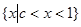 ,當c=1時,不等式的解集為
,當c=1時,不等式的解集為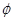 ,當c>1時,不等式的解集為
,當c>1時,不等式的解集為 。 ;(2)a<1+2
。 ;(2)a<1+2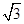
【解析】
試題分析:(1)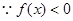
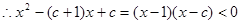 1分
1分
①當c<1時,
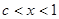
②當c=1時,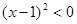 ,
,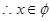
③當c>1時,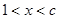 4分
4分
綜上,當c<1時,不等式的解集為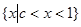 ,當c=1時,不等式的解集為
,當c=1時,不等式的解集為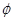 ,當c>1時,不等式的解集為
,當c>1時,不等式的解集為 。
5分
。
5分
(2)當c=-2時,f(x)>ax-5化為x2+x-2>ax-5
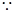 ax<x2+x+3,x∈(0,2)
恒成立
ax<x2+x+3,x∈(0,2)
恒成立
∴a<(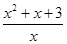 )min 設
)min 設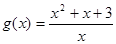 8分
8分
∴ ≥1+2
≥1+2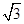 10分
10分
當且僅當x=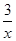 ,即x=
,即x=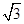 ∈(0,2)時,等號成立
∈(0,2)時,等號成立
∴g(x)min=(1+x+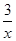 )min=1+2
)min=1+2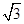
∴ a<1+2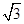 12分
12分
考點:本題考查了不等式的解法及恒成立問題的解法
點評:恒成立問題在解題過程中大致可分為以下幾種類型:
①一次函數型;②二次函數型;③變量分離型;④根據函數的奇偶性、周期性等性質;⑤直接根據函數的圖象。


科目:高中數學 來源: 題型:
| a |
| x |
| lnx |
| x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a |
| x |
| 3 |
| 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com