
正項(xiàng)數(shù)列 中,前n項(xiàng)和為
中,前n項(xiàng)和為 ,且
,且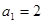 ,且
,且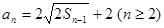 .
.
(1)求數(shù)列 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)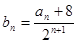 ,
,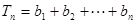 ,證明
,證明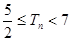 .
.
(1)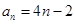 (2)
(2) ,利用錯(cuò)位相減法求得前n項(xiàng)和,依據(jù)和中
,利用錯(cuò)位相減法求得前n項(xiàng)和,依據(jù)和中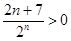 可知
可知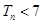 ,再結(jié)合數(shù)列是遞增的可知
,再結(jié)合數(shù)列是遞增的可知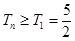
解析試題分析:(1) 由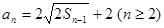 得
得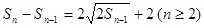
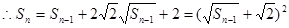 ,
,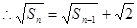
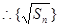 是首項(xiàng)為
是首項(xiàng)為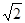 公差為
公差為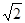 的等差數(shù)列,
的等差數(shù)列,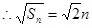 ,
, ,
, ,對(duì)n=1也成立,
,對(duì)n=1也成立,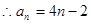
(2) ,
,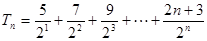
 ,兩式相減,得
,兩式相減,得

下面證明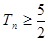 ,
, 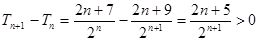 ,
,
或

 ,
,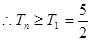 ,
,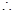
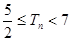
考點(diǎn):數(shù)列求通項(xiàng)求和
點(diǎn)評(píng):本題中求通項(xiàng)主要是由前n項(xiàng)和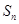 求
求 ,
, ,由已知條件先求得
,由已知條件先求得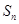 在求
在求 較簡(jiǎn)單,求和時(shí)應(yīng)用的錯(cuò)位相減法,這種方法適用于通項(xiàng)公式為n的一次式與指數(shù)式乘積的形式
較簡(jiǎn)單,求和時(shí)應(yīng)用的錯(cuò)位相減法,這種方法適用于通項(xiàng)公式為n的一次式與指數(shù)式乘積的形式



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知各項(xiàng)均不相等的等差數(shù)列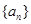 的前三項(xiàng)和為18,
的前三項(xiàng)和為18,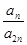 是一個(gè)與
是一個(gè)與 無關(guān)的常數(shù),若
無關(guān)的常數(shù),若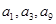 恰為等比數(shù)列
恰為等比數(shù)列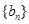 的前三項(xiàng),
的前三項(xiàng),
(1)求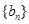 的通項(xiàng)公式.
的通項(xiàng)公式.
(2)記數(shù)列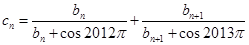 ,
,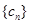 的前三
的前三 項(xiàng)和為
項(xiàng)和為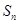 ,求證:
,求證: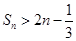
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知公比大于1的等比數(shù)列{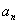 }滿足:
}滿足: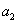 +
+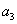 +
+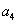 =28,且
=28,且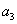 +2是
+2是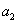 和
和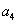 的等差中項(xiàng).(Ⅰ)求數(shù)列{
的等差中項(xiàng).(Ⅰ)求數(shù)列{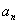 }的通項(xiàng)公式;
}的通項(xiàng)公式;
(Ⅱ)若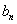 =
=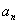
 ,求{
,求{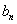 }的前n項(xiàng)和
}的前n項(xiàng)和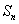 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
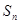 是等比數(shù)列
是等比數(shù)列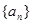 的前
的前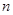 項(xiàng)和, 公比
項(xiàng)和, 公比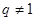 ,已知1是
,已知1是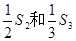 的等 差中項(xiàng),6是
的等 差中項(xiàng),6是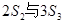 的等比中項(xiàng),
的等比中項(xiàng),
(1)求此數(shù)列的通項(xiàng)公式
(2)求數(shù)列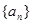 的前
的前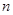 項(xiàng)和
項(xiàng)和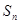
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本小題滿分12分)
等比數(shù)列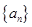 的各項(xiàng)均為正數(shù),且
的各項(xiàng)均為正數(shù),且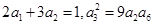
(1)求數(shù)列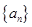 的通項(xiàng)公式.
的通項(xiàng)公式.
(2)設(shè) 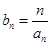 ,求數(shù)列
,求數(shù)列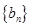 的前n項(xiàng)和
的前n項(xiàng)和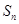 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
等比數(shù)列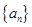 的各項(xiàng)均為正數(shù),且
的各項(xiàng)均為正數(shù),且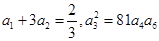
(1)求數(shù)列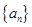 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)設(shè)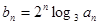 求數(shù)列
求數(shù)列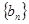 的前
的前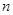 項(xiàng)和
項(xiàng)和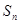 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
(本題滿分12分)設(shè)數(shù)列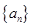 的前
的前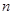 項(xiàng)和為
項(xiàng)和為 ,滿足
,滿足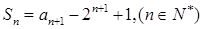 ,且
,且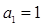 。
。
(Ⅰ)求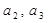 的值;
的值;
(Ⅱ)求數(shù)列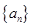 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅲ)設(shè)數(shù)列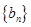 的前
的前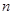 項(xiàng)和為
項(xiàng)和為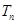 ,且
,且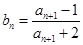 ,證明:對(duì)一切正整數(shù)
,證明:對(duì)一切正整數(shù)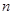 , 都有:
, 都有: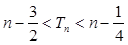
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
設(shè)同時(shí)滿足條件:①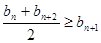 ;②
;②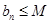 (
(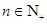 ,
,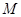 是與
是與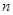 無關(guān)的常數(shù))的無窮數(shù)列
無關(guān)的常數(shù))的無窮數(shù)列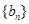 叫“嘉文”數(shù)列.已知數(shù)列
叫“嘉文”數(shù)列.已知數(shù)列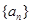 的前
的前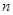 項(xiàng)和
項(xiàng)和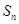 滿足:
滿足: 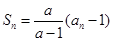 (
(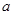 為常數(shù),且
為常數(shù),且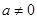 ,
,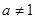 ).
).
(Ⅰ)求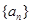 的通項(xiàng)公式;
的通項(xiàng)公式;
(Ⅱ)設(shè)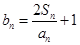 ,若數(shù)列
,若數(shù)列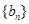 為等比數(shù)列,求
為等比數(shù)列,求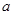 的值,并證明此時(shí)
的值,并證明此時(shí)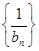 為“嘉文”數(shù)列.
為“嘉文”數(shù)列.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com