
【題目】在直角坐標系內(nèi),點A,B的坐標分別為![]() ,
,![]() ,P是坐標平面內(nèi)的動點,且直線
,P是坐標平面內(nèi)的動點,且直線![]() ,
,![]() 的斜率之積等于
的斜率之積等于![]() ,設(shè)點P的軌跡為C.
,設(shè)點P的軌跡為C.
(1)求軌跡C的方程;
(2)設(shè)過點![]() 且傾斜角不為0的直線
且傾斜角不為0的直線![]() 與軌跡C相交于M,N兩點,求證:直線
與軌跡C相交于M,N兩點,求證:直線![]() ,
,![]() 的交點在直線
的交點在直線![]() 上.
上.
【答案】(1)![]() ;(2)證明見解析.
;(2)證明見解析.
【解析】
(1)設(shè)點,列式,化簡(注意斜率存在的條件),求軌跡方程.
(2)直線![]() 傾斜角不為0,設(shè)直線的方程
傾斜角不為0,設(shè)直線的方程![]() (不用取討論斜率是否存在),聯(lián)立直線和橢圓的方程,消元,韋達定理,用點的坐標表示直線
(不用取討論斜率是否存在),聯(lián)立直線和橢圓的方程,消元,韋達定理,用點的坐標表示直線![]() 和
和![]() 方程,求交點
方程,求交點![]() ,進而求出
,進而求出![]() ,即證明交點在直線
,即證明交點在直線![]() .
.
(1)設(shè)點![]() ,
,![]() ,
,![]()
則![]() ,得
,得![]() ,即
,即![]() .
.
故軌跡C的方程為:![]() .
.
(2)根據(jù)題意,可設(shè)直線![]() 的方程為:
的方程為:![]() ,
,
由 ,消去x并整理得
,消去x并整理得![]() .
.
其中,![]() .
.
設(shè)![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
因直線![]() 的傾斜角不為0,故
的傾斜角不為0,故![]() ,
,![]() 不等于
不等于![]() (
(![]() ,
,![]() 不為0),
不為0),
從而可設(shè)直線![]() 的方程為:
的方程為:![]() ——①,
——①,
直線![]() 的方程為:
的方程為:![]() ——②,
——②,
所以,直線![]() ,
,![]() 的交點
的交點![]() 的坐標滿足:
的坐標滿足:
![]() .
.
而![]()
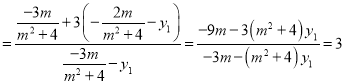 ,
,
因此,![]() ,即點Q在直線
,即點Q在直線![]() 上.
上.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數(shù)方程是
的參數(shù)方程是![]() (
(![]() 為參數(shù)),以原點
為參數(shù)),以原點![]() 為極點,以
為極點,以![]() 軸的非負半軸為極軸建立極坐標系,已知曲線
軸的非負半軸為極軸建立極坐標系,已知曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)過原點![]() 的直線
的直線![]() 與直線
與直線![]() 交于點
交于點![]() ,與曲線
,與曲線![]() 交于
交于![]() 、
、![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知雙曲線![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,
, ![]() 為坐標原點,
為坐標原點, ![]() 是雙曲線上在第一象限內(nèi)的點,直線
是雙曲線上在第一象限內(nèi)的點,直線![]() 分別交雙曲線
分別交雙曲線![]() 左、右支于另一點
左、右支于另一點![]() ,
, ![]() ,且
,且![]() ,則雙曲線
,則雙曲線![]() 的離心率為( )
的離心率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】網(wǎng)絡(luò)購物已經(jīng)成為人們的一種生活方式.某購物平臺為了給顧客提供更好的購物體驗,為入駐商家設(shè)置了積分制度,每筆購物完成后,買家可以根據(jù)物流情況、商品質(zhì)量等因素對商家做出評價,評價分為好評、中評和差評平臺規(guī)定商家有50天的試營業(yè)時間,期間只評價不積分,正式營業(yè)后,每個好評給商家計1分,中評計0分,差評計![]() 分,某商家在試營業(yè)期間隨機抽取100單交易調(diào)查了其商品的物流情況以及買家的評價情況,分別制成了圖1和圖2.
分,某商家在試營業(yè)期間隨機抽取100單交易調(diào)查了其商品的物流情況以及買家的評價情況,分別制成了圖1和圖2.
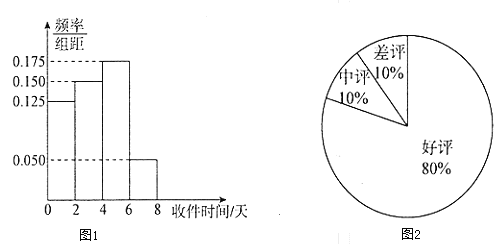
(1)通常收件時間不超過四天認為是物流迅速,否則認為是物流遲緩;
請根據(jù)題目所給信息完成下面![]() 列聯(lián)表,并判斷能否有
列聯(lián)表,并判斷能否有![]() 的把握認為“獲得好評”與物流速度有關(guān)?
的把握認為“獲得好評”與物流速度有關(guān)?
好評 | 中評或差評 | 合計 | |
物流迅速 | |||
物流遲緩 | 30 | ||
合計 |
(2)從正式營業(yè)開始,記商家在每筆交易中得到的評價得分為![]() .該商家將試營業(yè)50天期間的成交情況制成了頻數(shù)分布表(表1),以試營業(yè)期間成交單數(shù)的頻率代替正式營業(yè)時成交單數(shù)發(fā)生的概率.
.該商家將試營業(yè)50天期間的成交情況制成了頻數(shù)分布表(表1),以試營業(yè)期間成交單數(shù)的頻率代替正式營業(yè)時成交單數(shù)發(fā)生的概率.
表1
成交單數(shù) | 36 | 30 | 27 |
天數(shù) | 10 | 20 | 20 |
(Ⅰ)求![]() 的分布列和數(shù)學(xué)期望;
的分布列和數(shù)學(xué)期望;
(Ⅱ)平臺規(guī)定,當積分超過10000分時,商家會獲得“誠信商家”稱號,請估計該商家從正式營業(yè)開始,1年內(nèi)(365天)能否獲得“誠信商家”稱號
附: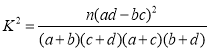
參考數(shù)據(jù):
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,四邊形
中,四邊形![]() 為梯形,
為梯形, ![]() ,且
,且![]() ,
, ![]() 是邊長為2的正三角形,頂點
是邊長為2的正三角形,頂點![]() 在
在![]() 上的射影為點
上的射影為點![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)證明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() 是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
是正三角形,CD平面PAD,E,F,G,O分別是PC,PD,BC,AD 的中點.
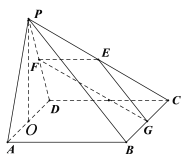
(Ⅰ)求證:PO平面![]() ;
;
(Ⅱ)求平面EFG與平面![]() 所成銳二面角的大小;
所成銳二面角的大小;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() ,使得直線
,使得直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,若存在,求線段
,若存在,求線段![]() 的長度;若不存在,說明理由.
的長度;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某車間用一臺包裝機包裝葡萄糖,每袋葡萄糖的重量是一個隨機變量,它服從正態(tài)分布.當機器工作正常時,每袋葡萄糖平均重量![]() 為0.5kg,標準差
為0.5kg,標準差![]() 為0.015kg.
為0.015kg.
(1)已知包裝每袋葡萄糖的成本為1元,若發(fā)現(xiàn)包裝好的葡萄糖重量異常,則需要將該袋葡萄糖進行重新包裝,假設(shè)重新包裝后的葡萄糖重量正常.若某袋葡萄糖的重量![]() 滿足
滿足![]() ,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應(yīng)成本的最小期望值.
,則認為該袋葡萄糖重量正常. 問:在機器工作正常的情況下,至少包裝多少袋葡萄糖才能使“至少有一袋包裝好的葡萄糖重量正常”的概率大于0.98?并求出相應(yīng)成本的最小期望值.
(2)某日開工后, 為檢査該包裝機工作是否正常, 隨機地抽取它所包裝的葡萄糖9袋,若抽取的9袋葡萄糖稱得凈重(kg)為:0.496, 0.508, 0.524, 0.519, 0.495, 0.510, 0.522, 0.513, 0.512.用樣本平均數(shù)![]() 作為
作為![]() 的估計值
的估計值![]() ,以
,以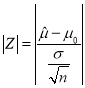 作為檢驗統(tǒng)計量,其中
作為檢驗統(tǒng)計量,其中![]() 為樣本總數(shù),
為樣本總數(shù),![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,且
,且![]() .
.
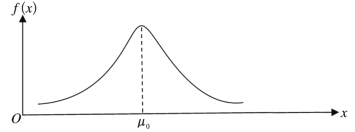
①若機器工作正常時, 每袋葡萄糖的重量服從的正態(tài)分布曲線如下圖所示,且經(jīng)計算得上述樣本數(shù)據(jù)的標準差![]() 0.022.請在下圖(機器正常工作時的正態(tài)分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態(tài)分布曲線的草圖.
0.022.請在下圖(機器正常工作時的正態(tài)分布曲線)中,繪制出以該樣本作為估計得到的每袋葡萄糖所服從的正態(tài)分布曲線的草圖.
②若![]() ,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過
,就推斷該包裝機工作異常,這種推斷犯錯誤的概率不超過![]() ,試以95%的可靠性估計該包裝機工作是否正常.
,試以95%的可靠性估計該包裝機工作是否正常.
附: 若隨機變量![]() 服從正態(tài)分布:
服從正態(tài)分布:![]() ,
,![]()
![]()
參考數(shù)據(jù):![]() ;
;![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在等差數(shù)列![]() 中,已知
中,已知![]() .在①
.在①![]() ,②
,②![]() ,③
,③![]() 這三個條件中任選一個補充在第(2)問中,并對其求解.
這三個條件中任選一個補充在第(2)問中,并對其求解.
(1)求數(shù)列![]() 的通項公式
的通項公式![]() ;
;
(2)若___________,求數(shù)列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com