
【題目】已知函數(shù)![]() ,其中
,其中![]() 是自然對(duì)數(shù)的底數(shù).
是自然對(duì)數(shù)的底數(shù).
(1)當(dāng)![]() 時(shí),求曲線
時(shí),求曲線![]() 在
在![]() 處的切線方程;
處的切線方程;
(2)如果對(duì)任意![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
(3)討論函數(shù)![]() 的零點(diǎn)個(gè)數(shù).
的零點(diǎn)個(gè)數(shù).
【答案】(1)![]() (2)
(2)![]() (3)當(dāng)
(3)當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有一個(gè)零點(diǎn);當(dāng)
有一個(gè)零點(diǎn);當(dāng)![]() 時(shí),
時(shí),![]() 有三個(gè)零點(diǎn).
有三個(gè)零點(diǎn).
【解析】
(1)代入![]() 的函數(shù)解析式,求得導(dǎo)函數(shù)及切點(diǎn)坐標(biāo),由導(dǎo)數(shù)的幾何意義即可得切線方程;
的函數(shù)解析式,求得導(dǎo)函數(shù)及切點(diǎn)坐標(biāo),由導(dǎo)數(shù)的幾何意義即可得切線方程;
(2)求得導(dǎo)函數(shù),并對(duì)![]() 分類討論,即可確定
分類討論,即可確定![]() 的單調(diào)性,進(jìn)而由不等式恒成立求得
的單調(diào)性,進(jìn)而由不等式恒成立求得![]() 的取值范圍;
的取值范圍;
(3)將![]() 的解析式代入可得
的解析式代入可得![]() 解析式,結(jié)合基本不等式可知在
解析式,結(jié)合基本不等式可知在![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有唯一零點(diǎn);當(dāng)
有唯一零點(diǎn);當(dāng)![]() 時(shí),可知
時(shí),可知![]() 為奇函數(shù),由
為奇函數(shù),由![]() 可判斷
可判斷![]() 的單調(diào)情況,進(jìn)而構(gòu)造
的單調(diào)情況,進(jìn)而構(gòu)造![]() ,可證明當(dāng)
,可證明當(dāng)![]() 時(shí),
時(shí),![]() ,進(jìn)而可知當(dāng)
,進(jìn)而可知當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有唯一零點(diǎn),即可判斷
有唯一零點(diǎn),即可判斷![]() 時(shí)
時(shí)![]() 的零點(diǎn)個(gè)數(shù).
的零點(diǎn)個(gè)數(shù).
(1)當(dāng)![]() 時(shí),
時(shí),![]() ,
,
可得![]() ,
,
則有![]() ,
,![]() ,即切點(diǎn)坐標(biāo)為
,即切點(diǎn)坐標(biāo)為![]() ,
,
則切線方程為![]() ,
,
化簡可得![]() .
.
(2)函數(shù)![]() ,
,
則![]() ,
,
當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,則函數(shù)
恒成立,則函數(shù)![]() 在
在![]() 上單增,而
上單增,而![]() ,與
,與![]() 恒成立矛盾,不合題意;
恒成立矛盾,不合題意;
當(dāng)![]() 時(shí),
時(shí),![]() 恒成立,則符合題意;
恒成立,則符合題意;
當(dāng)![]() 時(shí),由
時(shí),由![]() 得
得![]() ,則
,則![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
在![]() 上為單調(diào)遞增,
上為單調(diào)遞增,
則![]() ,解得
,解得![]() .
.
綜上:![]() .
.
(3)因![]() ,
,
當(dāng)![]() 時(shí),因?yàn)?/span>
時(shí),因?yàn)?/span>![]() 恒成立,
恒成立,
則![]() 在
在![]() 上為增函數(shù),而
上為增函數(shù),而![]() ,則此時(shí)函數(shù)
,則此時(shí)函數(shù)![]() 有唯一零點(diǎn).
有唯一零點(diǎn).
當(dāng)![]() 時(shí),
時(shí),![]() 則
則![]() 為奇函數(shù).
為奇函數(shù).
只需研究![]() 情形.
情形.
由![]() ,
,
得![]() ,則有
,則有![]() .
.
則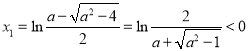 ,
,![]() ,
,
則![]() 在
在![]() 上為減函數(shù),在
上為減函數(shù),在![]() 上為增函數(shù),
上為增函數(shù),
則有![]() .
.
下面證明:當(dāng)![]() 時(shí),
時(shí),![]() .
.
證明:令![]() ,則
,則![]() ,
,![]() ,
,
即函數(shù)![]() 在
在![]() 上為增函數(shù),故有
上為增函數(shù),故有![]() ,
,
則![]() 在
在![]() 上為增函數(shù),故有
上為增函數(shù),故有![]() ,則
,則![]() .
.
當(dāng)![]() 時(shí),有
時(shí),有![]() ,則
,則![]() ,
,
取![]() ,則
,則![]() ,
,
因?yàn)?/span>![]() 為連續(xù)函數(shù),由零點(diǎn)存在性定理可得:存在唯一
為連續(xù)函數(shù),由零點(diǎn)存在性定理可得:存在唯一![]() ,使得
,使得![]() ,即當(dāng)
,即當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有唯一零點(diǎn),也即此時(shí)函數(shù)
有唯一零點(diǎn),也即此時(shí)函數(shù)![]() 有三個(gè)零點(diǎn).
有三個(gè)零點(diǎn).
綜上:當(dāng)![]() 時(shí),函數(shù)
時(shí),函數(shù)![]() 有一個(gè)零點(diǎn);當(dāng)
有一個(gè)零點(diǎn);當(dāng)![]() 時(shí),
時(shí),![]() 有三個(gè)零點(diǎn).
有三個(gè)零點(diǎn).


 一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術(shù)出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)橢圓E:![]() +
+![]() =1(a>b>0)的左、右焦點(diǎn)分別為F1,F2,過點(diǎn)F1的直線交橢圓E于A,B兩點(diǎn).若橢圓E的離心率為
=1(a>b>0)的左、右焦點(diǎn)分別為F1,F2,過點(diǎn)F1的直線交橢圓E于A,B兩點(diǎn).若橢圓E的離心率為![]() ,三角形ABF2的周長為4
,三角形ABF2的周長為4![]() .
.
(1)求橢圓E的方程;
(2)設(shè)不經(jīng)過橢圓的中心而平行于弦AB的直線交橢圓E于點(diǎn)C,D,設(shè)弦AB,CD的中點(diǎn)分別為M,N,證明:O,M,N三點(diǎn)共線.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為實(shí)現(xiàn)2020年全面建設(shè)小康社會(huì),某地進(jìn)行產(chǎn)業(yè)的升級(jí)改造.經(jīng)市場(chǎng)調(diào)研和科學(xué)研判,準(zhǔn)備大規(guī)模生產(chǎn)某高科技產(chǎn)品的一個(gè)核心部件,目前只有甲、乙兩種設(shè)備可以獨(dú)立生產(chǎn)該部件.如圖是從甲設(shè)備生產(chǎn)的部件中隨機(jī)抽取400件,對(duì)其核心部件的尺寸x,進(jìn)行統(tǒng)計(jì)整理的頻率分布直方圖.
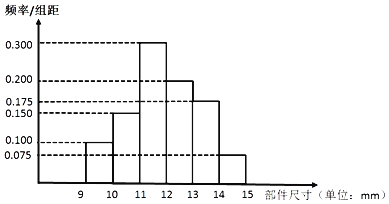
根據(jù)行業(yè)質(zhì)量標(biāo)準(zhǔn)規(guī)定,該核心部件尺寸x滿足:|x﹣12|≤1為一級(jí)品,1<|x﹣12|≤2為二級(jí)品,|x﹣12|>2為三級(jí)品.
(Ⅰ)現(xiàn)根據(jù)頻率分布直方圖中的分組,用分層抽樣的方法先從這400件樣本中抽取40件產(chǎn)品,再從所抽取的40件產(chǎn)品中,抽取2件尺寸x∈[12,15]的產(chǎn)品,記ξ為這2件產(chǎn)品中尺寸x∈[14,15]的產(chǎn)品個(gè)數(shù),求ξ的分布列和數(shù)學(xué)期望;
(Ⅱ)將甲設(shè)備生產(chǎn)的產(chǎn)品成箱包裝出售時(shí),需要進(jìn)行檢驗(yàn).已知每箱有100件產(chǎn)品,每件產(chǎn)品的檢驗(yàn)費(fèi)用為50元.檢驗(yàn)規(guī)定:若檢驗(yàn)出三級(jí)品需更換為一級(jí)或二級(jí)品;若不檢驗(yàn),讓三級(jí)品進(jìn)入買家,廠家需向買家每件支付200元補(bǔ)償.現(xiàn)從一箱產(chǎn)品中隨機(jī)抽檢了10件,結(jié)果發(fā)現(xiàn)有1件三級(jí)品.若將甲設(shè)備的樣本頻率作為總體的慨率,以廠家支付費(fèi)用作為決策依據(jù),問是否對(duì)該箱中剩余產(chǎn)品進(jìn)行一一檢驗(yàn)?請(qǐng)說明理由;
(Ⅲ)為加大升級(jí)力度,廠家需增購設(shè)備.已知這種產(chǎn)品的利潤如下:一級(jí)品的利潤為500元/件;二級(jí)品的利潤為400元/件;三級(jí)品的利潤為200元/件.乙種設(shè)備產(chǎn)品中一、二、三級(jí)品的概率分別是![]() ,
,![]() ,
,![]() .若將甲設(shè)備的樣本頻率作為總體的概率,以廠家的利潤作為決策依據(jù).應(yīng)選購哪種設(shè)備?請(qǐng)說明理由.
.若將甲設(shè)備的樣本頻率作為總體的概率,以廠家的利潤作為決策依據(jù).應(yīng)選購哪種設(shè)備?請(qǐng)說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,設(shè)內(nèi)角
中,設(shè)內(nèi)角![]() ,
,![]() ,
,![]() 的對(duì)邊分別為
的對(duì)邊分別為![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() ,
,![]() 成等比數(shù)列,求證:
成等比數(shù)列,求證:![]() ;
;
(2)若![]() (
(![]() 為銳角),
為銳角),![]() .求
.求![]() 中
中![]() 邊上的高
邊上的高![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知集合M是滿足下列性質(zhì)的函數(shù)f(x)的全體:存在非零常數(shù)T,對(duì)任意x∈R,有f(x+T)=Tf(x)成立.
(1)函數(shù)f(x)=x是否屬于集合M?說明理由;
(2)設(shè)函數(shù)f(x)=ax(a>0,且a≠1)的圖象與y=x的圖象有公共點(diǎn),證明:f(x)=ax∈M;
(3)若函數(shù)f(x)=sinkx∈M,求實(shí)數(shù)k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
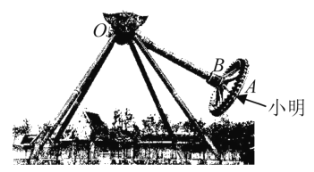
【題目】如圖,大擺錘是一種大型的游樂設(shè)備,常見于各大游樂園.游客坐在圓形的座艙中,面向外.通常,大擺錘以壓肩作為安全束縛,配以安全帶作為二次保險(xiǎn).座艙旋轉(zhuǎn)的同時(shí),懸掛座艙的主軸在電機(jī)的驅(qū)動(dòng)下做單擺運(yùn)動(dòng).大擺錘的運(yùn)行可以使置身其上的游客驚心動(dòng)魄.今年元旦,小明去某游樂園玩“大擺錘”,他坐在點(diǎn)![]() 處,“大擺錘”啟動(dòng)后,主軸
處,“大擺錘”啟動(dòng)后,主軸![]() 在平面
在平面![]() 內(nèi)繞點(diǎn)
內(nèi)繞點(diǎn)![]() 左右擺動(dòng),平面
左右擺動(dòng),平面![]() 與水平地面垂直,
與水平地面垂直,![]() 擺動(dòng)的過程中,點(diǎn)
擺動(dòng)的過程中,點(diǎn)![]() 在平面
在平面![]() 內(nèi)繞點(diǎn)
內(nèi)繞點(diǎn)![]() 作圓周運(yùn)動(dòng),并且始終保持
作圓周運(yùn)動(dòng),并且始終保持![]() ,
,![]() ,已知
,已知![]() ,在“大擺錘”啟動(dòng)后,下列
,在“大擺錘”啟動(dòng)后,下列![]() 個(gè)結(jié)論中正確的是______(請(qǐng)?zhí)钌纤姓_結(jié)論的序號(hào)).
個(gè)結(jié)論中正確的是______(請(qǐng)?zhí)钌纤姓_結(jié)論的序號(hào)).
①點(diǎn)![]() 在某個(gè)定球面上運(yùn)動(dòng);
在某個(gè)定球面上運(yùn)動(dòng);
②線段![]() 在水平地面上的正投影的長度為定值;
在水平地面上的正投影的長度為定值;
③直線![]() 與平面
與平面![]() 所成角的正弦值的最大值為
所成角的正弦值的最大值為![]() ;
;
④直線![]() 與平面
與平面![]() 所成角的正弦值的最大值為
所成角的正弦值的最大值為![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某單位一輛交通車載有8個(gè)職工從單位出發(fā)送他們下班回家,途中共有甲、乙、丙3個(gè)停車點(diǎn).如果某停車點(diǎn)無人下車,那么該車在這個(gè)點(diǎn)就不停車.假設(shè)每個(gè)職工在每個(gè)停車點(diǎn)下車的可能性都是相等的,求下列事件的概率:
(1)該車在某停車點(diǎn)停車;
(2)停車的次數(shù)不少于2次;
(3)恰好停車2次.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com