
【題目】拉丁舞,又稱拉丁風情舞或自由社交舞,它是拉丁人民在漫長的歷史長河中形成的,包含倫巴、恰恰、牛仔舞、桑巴、斗牛舞、深受人民的喜愛.某藝術培訓機構為了調查本校學院對拉丁舞的學習情況,分別在剛學習了一個季度的本校大班(8歲以下)及種子班(8歲以上)的學員中各隨機抽取了15名學員進行摸底考試,這30名學員考試成績的莖葉圖如圖所示.

規定:成績不低于85分,則認為成績優秀;成績低于85分,則認為成績一般.
(1)根據上述數據填寫下列2×2聯表:
成績優秀 | 成績一般 | 總計 | |
大班 | |||
種子班 | |||
總計 |
判斷是否有95%的把握認為成績優秀或成績一般與學員的年齡有關;
(2)在大班及種子班的參加摸底考試且成績優秀的學員中以分層抽樣的方式抽取6名學員進行特別集訓,集訓后,再對這6名學員進行測試,按測試成績,取前3名授予“舞蹈小精靈”稱號,在被授予“舞蹈小精靈”稱號的學員中,求種子班的學員恰好有2人的概率.
參考公式及數據: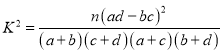 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【答案】(1)列聯表見解析,有;(2)![]() .
.
【解析】
(1)先閱讀題意,再分析數據,填寫列聯表即可;
(2)由莖葉圖中的數據,分別列出所求事件的基本事件,然后結合古典概型概率公式求解即可.
解:(1)由莖葉圖的數據,填寫2×2列聯表如下:
成績優秀 | 成績一般 | 總計 | |
大班 | 6 | 9 | 15 |
種子班 | 12 | 3 | 15 |
總計 | 18 | 12 | 30 |
根據列聯表中的數據,得到![]()
因此有95%的把握認為成績優秀或成績一般與學員的年齡有關.
(2)由莖葉圖中的數據可知,大班學員中成績優秀的人數為6,種子班學員中成績優秀的人數為12,以分層抽樣的方式抽取6人,則大班抽取的人數為![]() ,記為
,記為![]() ,
,
種子班抽取的人數為![]() ,記為
,記為![]() ,
,
則被授予“舞蹈小精靈”稱號的基本事件有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共20個,
,共20個,
其中種子班學員的人數恰有2人的基本時間有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共12個,
,共12個,
故被授予“舞蹈小精靈”稱號的學員中,求種子班的學員恰好有2人的概率為![]() .
.


 口算題天天練系列答案
口算題天天練系列答案科目:高中數學 來源: 題型:
【題目】為了美化校園,要對校園內某一區域作如下設計,如圖,已知![]() ,
,![]() ,
,![]() ,在邊BC上選一點P. 沿著AP和CP重新栽種花木,圖中陰影部分鋪上草坪. AP段栽種花木費用是每米3a元,CP段栽種花木費用是每米2a元,其中a是正常數.設
,在邊BC上選一點P. 沿著AP和CP重新栽種花木,圖中陰影部分鋪上草坪. AP段栽種花木費用是每米3a元,CP段栽種花木費用是每米2a元,其中a是正常數.設![]() .
.
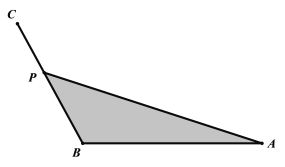
(1)求栽種花木費用y關于θ的函數表達式;
(2)求![]() 的值,使得栽種花木費用y最小.
的值,使得栽種花木費用y最小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 是公差為d(
是公差為d(![]() )的等差數列,它的前n項和記為
)的等差數列,它的前n項和記為![]() ,數列
,數列![]() 是公比為q(
是公比為q(![]() )的等比數列,它的前n項和記為
)的等比數列,它的前n項和記為![]() .若
.若![]() ,且存在不小于3的正整數
,且存在不小于3的正整數![]() ,使
,使![]() .
.
(1)若![]() ,求
,求![]() .
.
(2)若![]() 試比較
試比較![]() 與
與![]() 的大小,并說明理由;
的大小,并說明理由;
(3)若![]() ,是否存在整數m,k,使
,是否存在整數m,k,使![]() 若存在,求出m,k的值;若不存在,說明理由.
若存在,求出m,k的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,已知直線
中,已知直線![]() 的直角坐標方程為
的直角坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以直角坐標系原點為極點,
為參數),以直角坐標系原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 和直線
和直線![]() 的極坐標方程;
的極坐標方程;
(2)已知直線![]() 與曲線
與曲線![]() 、
、![]() 相交于異于極點的點
相交于異于極點的點![]() ,若
,若![]() 的極徑分別為
的極徑分別為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 的底面為直角梯形,
的底面為直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,二面角
,二面角![]() 的大小為
的大小為![]() ,
,![]() ,
,![]() 為線段
為線段![]() 的中點,
的中點,![]() 為線段
為線段![]() 上的動點.
上的動點.
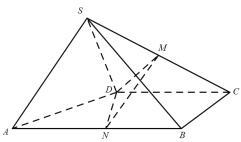
(1)求證:平面![]() 平面
平面![]() ;
;
(2)是否存在點![]() ,使二面角
,使二面角![]() 的大小為
的大小為![]() ,若存在,求
,若存在,求![]() 的值,不存在說出理由.
的值,不存在說出理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,
為坐標原點,![]() ,
,![]() ,
,![]() ,若
,若![]() .
.
⑴ 求函數![]() 的最小正周期和單調遞增區間;
的最小正周期和單調遞增區間;
⑵ 將函數![]() 的圖象上各點的橫坐標伸長為原來的
的圖象上各點的橫坐標伸長為原來的![]() 倍(縱坐標不變),再將得到的圖象向左平移
倍(縱坐標不變),再將得到的圖象向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象,求函數
的圖象,求函數![]() 在
在![]() 上的最小值.
上的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com