
【題目】已知數集![]() 具有性質
具有性質![]() ;對任意的
;對任意的![]() 、
、![]() ,
,![]() ,與
,與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() .
.
(1)分別判斷數集![]() 與
與![]() 是否具有性質
是否具有性質![]() ,并說明理由;
,并說明理由;
(2)證明:![]() ,且
,且![]() ;
;
(3)當![]() 時,若
時,若![]() ,求集合
,求集合![]() .
.
【答案】(1) 集合![]() 具有性質
具有性質![]() ,集合
,集合![]() 不具有性質
不具有性質![]() .(2)證明見解析.(3)
.(2)證明見解析.(3)![]() .
.
【解析】
(1)利用![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() .即可判斷出結論.
.即可判斷出結論.
(2)令“![]() ,由“
,由“![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() ”可得
”可得![]() 屬于
屬于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某項,
中某項,![]() 不符合不符合題意,
不符合不符合題意,![]() 符合.同理可得:令
符合.同理可得:令![]() 可以得到
可以得到![]() ,令
,令![]() ,
,![]() 可以得到
可以得到![]() ,倒序相加即可.
,倒序相加即可.
(3)當![]() 時,取
時,取![]() ,當
,當![]() 時,
時,![]() ,由A具有性質P,
,由A具有性質P,![]() ,又
,又![]() 時,
時,![]() ,可得
,可得![]()
![]() ,則
,則![]() ,又
,又![]() ,可得
,可得![]() ,則
,則![]() ,則有
,則有![]() .可得即
.可得即![]() 是首項為
是首項為![]() ,公差為
,公差為![]() 等差數列是首項為0,公差為
等差數列是首項為0,公差為![]() 等差數列.
等差數列.
解:(1)在集合![]() 中,設
中,設![]()
①![]() ,具有性質
,具有性質![]()
②![]() ,具有性質
,具有性質![]()
③![]() ,具有性質
,具有性質![]()
④![]() ,具有性質
,具有性質![]()
⑤![]() ,具有性質
,具有性質![]()
⑥![]() ,具有性質
,具有性質![]()
綜上所述:集合![]() 具有性質
具有性質![]() ;
;
在集合![]() 中,設
中,設![]() ,
,
①![]() ,具有性質
,具有性質![]()
②![]() ,具有性質
,具有性質![]()
③![]() ,具有性質
,具有性質![]()
④![]() ,不具有性質
,不具有性質![]()
⑤![]() ,具有性質
,具有性質![]()
⑥![]() ,具有性質
,具有性質![]()
綜上所述:集合![]() 不具有性質
不具有性質![]() .
.
故集合![]() 具有性質
具有性質![]() ,集合
,集合![]() 不具有性質
不具有性質![]() .
.
(2) 證明:令![]()
![]() ,
,
則![]() 與
與![]() 兩數中至少有一個屬于
兩數中至少有一個屬于![]() ”,
”,
![]() 不屬于
不屬于![]() ,
,![]() 屬于
屬于![]() .
.
令![]() ,那么
,那么![]() 是集合
是集合![]() 中某項,
中某項,![]() 不符合題意,
不符合題意,![]() 可以.
可以.
如果是![]() 或者
或者![]() ,那么可知
,那么可知![]() ,
,
那么![]() ,只能是等于
,只能是等于![]() ,矛盾.
,矛盾.
所以令![]() 可以得到
可以得到![]() ,
,
同理,令![]() ,
,![]() 可以得到
可以得到![]() ,
,
![]() 倒序相加即可得到
倒序相加即可得到![]()
即![]()
(3)當![]() 時,取
時,取![]() ,當
,當![]() 時,
時,![]() ,
,
由![]() 具有性質
具有性質![]() ,
,![]() ,又
,又![]() 時,
時,![]() ,
,
![]()
![]() ,
,
![]() ,
,
則![]() ,
,
![]() ,
,
從而可得![]() ,
,
故![]() ,即
,即![]() ,
,
又![]()
![]()
,則![]() ,則有
,則有![]()
又![]()
![]() ,
,
即![]() 是首項為
是首項為![]() ,公差為
,公差為![]() 等差數列,
等差數列,
![]()


科目:高中數學 來源: 題型:
【題目】現有一塊大型的廣告宣傳版面,其形狀是右圖所示的直角梯形![]() .某廠家因產品宣傳的需要,擬投資規劃出一塊區域(圖中陰影部分)為產品做廣告,形狀為直角梯形
.某廠家因產品宣傳的需要,擬投資規劃出一塊區域(圖中陰影部分)為產品做廣告,形狀為直角梯形![]() (點
(點![]() 在曲線段
在曲線段![]() 上,點
上,點![]() 在線段
在線段![]() 上).已知
上).已知![]() ,
, ![]() ,其中曲線段
,其中曲線段![]() 是以
是以![]() 為頂點,
為頂點, ![]() 為對稱軸的拋物線的一部分.
為對稱軸的拋物線的一部分.
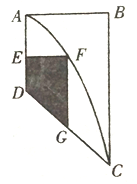
(1)建立適當的平面直角坐標系,分別求出曲線段![]() 與線段
與線段![]() 的方程;
的方程;
(2)求該廠家廣告區域![]() 的最大面積.
的最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左右焦點分別為
的左右焦點分別為![]() ,
, ![]() 上的動點
上的動點![]() 到兩焦點的距離之和為4,當點
到兩焦點的距離之和為4,當點![]() 運動到橢圓
運動到橢圓![]() 的上頂點時,直線
的上頂點時,直線![]() 恰與以原點
恰與以原點![]() 為圓心,以橢圓
為圓心,以橢圓![]() 的離心率為半徑的圓相切.
的離心率為半徑的圓相切.
(1)求橢圓![]() 的方程;
的方程;
(2)設橢圓![]() 的左右頂點分別為
的左右頂點分別為![]() ,若
,若![]() 交直線
交直線![]() 于
于![]() 兩點.問以
兩點.問以![]() 為直徑的圓是否過定點?若過定點,請求出該定點坐標;若不過定點,請說明理由.
為直徑的圓是否過定點?若過定點,請求出該定點坐標;若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中生調查了當地某小區的50戶居民由于臺風造成的經濟損失,將收集的數據分成![]() 三組,并作出如下頻率分布直方圖:
三組,并作出如下頻率分布直方圖:

(1)在直方圖的經濟損失分組中,以各組的區間中點值代表該組的各個值,并以經濟損失落入該區間的頻率作為經濟損失取該區間中點值的概率(例如:經濟損失![]() 則取
則取![]() ,且
,且![]() 的概率等于經濟損失落入
的概率等于經濟損失落入![]() 的頻率)。現從當地的居民中隨機抽出2戶進行捐款援助,設抽出的2戶的經濟損失的和為
的頻率)。現從當地的居民中隨機抽出2戶進行捐款援助,設抽出的2戶的經濟損失的和為![]() ,求
,求![]() 的分布列和數學期望.
的分布列和數學期望.
(2)臺風后居委會號召小區居民為臺風重災區捐款,此高中生調查的50戶居民捐款情況如下表,在表格空白處填寫正確數字,并說明是否有95%以上的把握認為捐款數額多于或少于500元和自身經濟損失是否到4000元有關?
經濟損失不超過4000元 | 經濟損失超過4000元 | 合計 | |
捐款超過500元 | 30 | ||
捐款不超過500元 | 6 | ||
合計 |
附:臨界值表參考公式:  .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的內接等邊三角形
的內接等邊三角形![]() 的面積為
的面積為![]() (其中
(其中![]() 為坐標原點).
為坐標原點).
(1)試求拋物線![]() 的方程;
的方程;
(2)已知點![]() 兩點在拋物線
兩點在拋物線![]() 上,
上,![]() 是以點
是以點![]() 為直角頂點的直角三角形.
為直角頂點的直角三角形.
①求證:直線![]() 恒過定點;
恒過定點;
②過點![]() 作直線
作直線![]() 的垂線交
的垂線交![]() 于點
于點![]() ,試求點
,試求點![]() 的軌跡方程,并說明其軌跡是何種曲線.
的軌跡方程,并說明其軌跡是何種曲線.
查看答案和解析>>
科目:高中數學 來源: 題型:
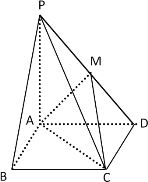
【題目】如圖,在四棱錐P-ABCD中,底面ABCD是矩形, M為PD的中點,PA⊥平面ABCD,PA=AD= 4, AB = 2.
(1)求證:AM⊥平面MCD;
(2)求直線PC與平面MAC所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】計劃在某水庫建一座至多安裝4臺發電機的水電站,過去0年的水文資料顯示,水庫年入流量![]() (年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,其中,不足80的年份有10年,不低于80且不足120的年份有30年,不低于120且不足160的年份有8年,不低于160的年份有2年,將年入流量在以上四段的頻率作為相應段的概率,并假設各年的年入流量相互獨立.
(年入流量:一年內上游來水與庫區降水之和,單位:億立方米)都在40以上,其中,不足80的年份有10年,不低于80且不足120的年份有30年,不低于120且不足160的年份有8年,不低于160的年份有2年,將年入流量在以上四段的頻率作為相應段的概率,并假設各年的年入流量相互獨立.
(1)求在未來3年中,至多1年的年入流量不低于120的概率;
(2)水電站希望安裝的發電機盡可能運行,但每年發電機最多可運行臺數受年入流量![]() 的限制,并有如下關系:
的限制,并有如下關系:
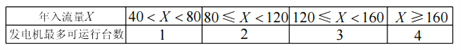
若某臺發電機運行,則該臺發電機年利潤為500萬元;若某臺發電機未運行,則該臺發電機年虧損1500萬元,水電站計劃在該水庫安裝2臺或3臺發電機,你認為應安裝2臺還是3臺發電機?請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】假設關于某設備的使用年限x(年)和所支出的維修費用y(萬元)有如下的統計資料:
x | 2 | 3 | 4 | 5 | 6 |
y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)畫出散點圖并判斷是否線性相關;
(2)如果線性相關,求線性回歸方程;
(3)估計使用年限為10年時,維修費用是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com