用數(shù)學歸納法證明:

能被9整除.

1)當
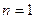
時,
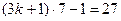
,能被9整除,命題成立.
(2)假設當

時,

能被9整除,當
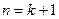
時,

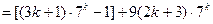

和
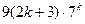
都能被9整除.
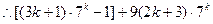
都能被9整除.
即
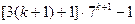
能被9整除.
即當
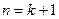
時,命題成立.
由(1)、(2)可知,對任何

命題都成立.
證明一個與
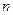
有關(guān)的式子
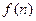
能被一個數(shù)
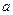
(或一個代數(shù)式

)整除,主要是找到
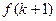
與

的關(guān)系,設法找到式子
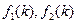
,使得
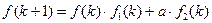
,就可證昨命題成立.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
是否存在常數(shù)a、b、c使等式12+22+32+…+n2+(n-1)2+…+22+12=an(bn2+c)對于一切n∈N*都成立,若存在,求出a、b、c并證明;若不存在,試說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
用數(shù)學歸納法證明:對一切大于1的自然數(shù),不等式(1+
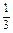
)(1+
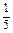
)…(1+

)>
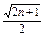
均成立.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
用數(shù)學歸納法證明
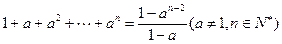
,在驗證n=1時,左邊計算所得的式子是()
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
若

,則

的最大值為______.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
用數(shù)學歸納法證明3
k≥
n3(
n≥3,
n∈N)第一步應驗證( )
| A.n="1" | B.n="2" | C.n="3" | D.n=4 |
查看答案和解析>>

 能被9整除.
能被9整除.