【題目】已知在
中，角
的對邊分別是
，且有
.
（1）求
；
（2）若
，求
面積的最大值.
【答案】(1) 
；(2) 
.
【解析】試題分析：（Ⅰ）已知等式利用正弦定理化簡，利用兩角和與差的正弦函數公式及誘導公式，結合sinC不為0求出cosC的值，即可確定出C的度數；
（2）利用余弦定理列出關系式，結合不等式可得ab≤9，進而求得
面積的最大值.
試題解析：∵在△ABC中，0＜C＜π，∴sinC≠0
已知等式利用正弦定理化簡得：2cosC（sinAcosB+sinBcosA）=sinC，
整理得：2cosCsin（A+B）=sinC，
即2cosCsin（π-（A+B））=sinC
2cosCsinC=sinC
∴cosC=
，
C∈（0，π）.
∴C=
.
（2）由余弦定理可得：9=c2=a2+b2-2abcosC≥2ab-ab=ab，
可得ab≤9，
S=absinC≤
當且僅當a=b=3時取等號
∴△ABC面積的最大值
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】某市政府為了節約生活用電，計劃在本市試行居民生活用電定額管理，即確定一個居民月用電量標準
，用電量不超過
的部分按平價收費，超出
的部分按議價收費．為此，政府調查了100戶居民的月平均用電量（單位：度），以
， 
， 
， 
， 
， 
， 
分組的頻率分布直方圖如圖所示．
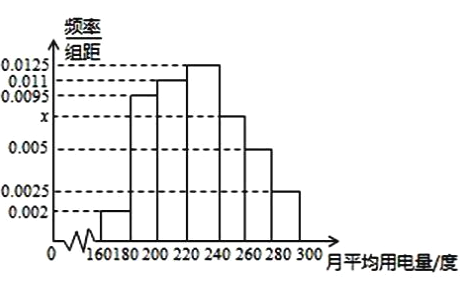
（1）求直方圖中
的值；
（2）求月平均用電量的眾數和中位數；
（3）如果當地政府希望使
左右的居民每月的用電量不超出標準，根據樣本估計總體的思想，你認為月用電量標準
應該定為多少合理？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，三棱柱
中，底面
為正三角形， 
底面
，且
， 
是
的中點.
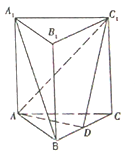
（1）求證： 
平面
；
（2）求證：平面
平面
；
（3）在側棱
上是否存在一點
，使得三棱錐
的體積是
？若存在，求出
的長；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】若平面點集
滿足：任意點
，存在
，都有
，則稱該點集
是“
階聚合”點集。現有四個命題：
①若
，則存在正數
，使得
是“
階聚合”點集；
②若
，則
是“
階聚合”點集；
③若
，則
是“2階聚合”點集；
④若
是“
階聚合”點集，則
的取值范圍是
.
其中正確命題的序號為（ ）
A. ①④ B. ②③ C. ①② D. ③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在三棱柱
中， 
底面
， 
， 
， 
， 
是棱
上一點．
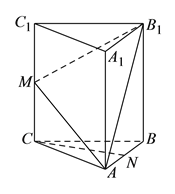
（I）求證： 
．
（II）若
， 
分別是
， 
的中點，求證： 
平面
．
（III）若二面角
的大小為
，求線段
的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知過點A(0，1)且斜率為k的直線l與圓C：(x－2)2＋(y－3)2＝1交于M，N兩點．
(1)求k的取值范圍；
(2)若
＝12，其中O為坐標原點，求|MN|.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直角坐標系
中，橢圓
的上焦點為
，橢圓
的離心率為
，且過點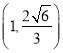
.
（1）求橢圓
的方程.
（2）設過橢圓
的上頂點
的直線
與橢圓
交于點
（
不在
軸上），垂直于
的直線與
交于點
，與
軸交于點
，若
，且
，求直線
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
