
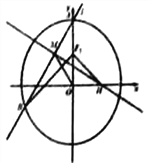
【題目】如圖,在直角坐標系![]() 中,橢圓
中,橢圓![]() 的上焦點為
的上焦點為![]() ,橢圓
,橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點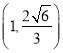 .
.
(1)求橢圓![]() 的方程.
的方程.
(2)設過橢圓![]() 的上頂點
的上頂點![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 交于點
交于點![]() (
(![]() 不在
不在![]() 軸上),垂直于
軸上),垂直于![]() 的直線與
的直線與![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,若
,若![]() ,且
,且![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1)![]() ;(2)直線
;(2)直線![]() 的方程為
的方程為![]() .
.
【解析】試題分析:(1)根據橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 ,結合性質
,結合性質![]() ,列出關于
,列出關于![]() 、
、![]() 、
、![]() 的方程組,求出
的方程組,求出![]() 、
、![]() 、
、![]() ,即可求得橢圓
,即可求得橢圓![]() 的標準方程;(2)設直線
的標準方程;(2)設直線![]() 的方程為
的方程為![]() ,由
,由 ,求得
,求得![]() 點坐標,求得
點坐標,求得![]() 點坐標,根據向量數量積的坐標運算列方程求得
點坐標,根據向量數量積的坐標運算列方程求得![]() ,即可求得直線
,即可求得直線![]() 的方程.
的方程.
試題解析:(1)因為橢圓的離心率為![]() ,所以
,所以![]()
即可得![]() ,所以橢圓
,所以橢圓![]() 的方程為
的方程為 ,
,
把點 代入
代入![]() 中,
中,
解得![]()
所以橢圓方程為![]()
(2)設直線![]() 的斜率為
的斜率為![]() ,
,
則直線![]() 的方程為
的方程為![]()
由
設由(1)知![]() ,設
,設![]() ,
,
則有![]()
所以![]() 所以
所以
因為![]() ,所以
,所以![]() 在線段
在線段![]() 的中垂線上.
的中垂線上.
所以![]() ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,
,
設![]() ,又直線
,又直線![]() 垂直
垂直![]()
∴
∴![]() ,即
,即
又![]() ∴
∴ ,
, ![]()
又![]() ∴
∴![]()
![]()
所以直線![]() 的方程為
的方程為![]() .
.
【方法點晴】本題主要考查待定系數求橢圓方程以及直線與橢圓的位置關系和數量積公式,屬于難題.用待定系數法求橢圓方程的一般步驟;①作判斷:根據條件判斷橢圓的焦點在![]() 軸上,還是在
軸上,還是在![]() 軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程
軸上,還是兩個坐標軸都有可能;②設方程:根據上述判斷設方程![]() 或
或![]()
![]() ;③找關系:根據已知條件,建立關于
;③找關系:根據已知條件,建立關于![]() 、
、![]() 、
、![]() 的方程組;④得方程:解方程組,將解代入所設方程,即為所求.
的方程組;④得方程:解方程組,將解代入所設方程,即為所求.


科目:高中數學 來源: 題型:
【題目】如圖,四棱錐![]() 中,底面
中,底面![]() 為平行四邊形,
為平行四邊形, ![]() ,
, ![]() 是棱PD的中點,且
是棱PD的中點,且![]() ,
, ![]() .
.
(I)求證: ![]() ; (Ⅱ)求二面角
; (Ⅱ)求二面角![]() 的大小;
的大小;
(Ⅲ)若![]() 是
是![]() 上一點,且直線
上一點,且直線![]() 與平面
與平面![]() 成角的正弦值為
成角的正弦值為![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】4月23日是“世界讀書日”,某中學在此期間開展了一系列的讀書教育活動,為了解本校學生課外閱讀情況,學校隨機抽取了100名學生對其課外閱讀時間進行調查,下面是根據調查結果繪制的學生日均課外閱讀時間(單位:min)的頻率分布直方圖,若將日均課外閱讀時間不低于60 min的學生稱為“書蟲”,低于60 min的學生稱為“懶蟲”,

(1)求x的值并估計全校3 000名學生中“書蟲”大概有多少名學生?(將頻率視為概率)
(2)根據已知條件完成下面2×2的列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“書蟲”與性別有關:

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年9月3日,抗戰勝利71周年紀念活動在北京隆重舉行,受到全國人民的矚目.紀念活動包括舉行紀念大會、閱兵式、擁待會和文藝晚會等,據統計,抗戰老兵由于身體原因,參加紀念大會、閱兵式、招待會這個環節(可參加多個,也可都不參加)的情況及其概率如下表所示:

(Ⅰ)若m=2n,則從這60名抗戰老兵中按照參加紀念活動的環節數分層抽取6人進行座談,求從參加紀念活動環節數為1的抗戰老兵中抽取的人數;
(Ⅱ)某醫療部門決定從(Ⅰ)中抽取的6名抗戰老兵中隨機抽取2名進行體檢,求這2名抗戰老兵中至少有1人參加紀念活動的環節數為3的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓x2+![]() =1(0<b<1)的左焦點為F,左、右頂點分別為A、C,上頂點為B,過F、B、C三點作圓P,其中圓心P的坐標為(m,n).
=1(0<b<1)的左焦點為F,左、右頂點分別為A、C,上頂點為B,過F、B、C三點作圓P,其中圓心P的坐標為(m,n).
(1)若FC是圓P的直徑,求橢圓的離心率;
(2)若圓P的圓心在直線x+y=0上,求橢圓的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】經統計,某校學生上學路程所需要時間全部介于![]() 與
與![]() 之間(單位:分鐘).現從在校學生中隨機抽取
之間(單位:分鐘).現從在校學生中隨機抽取![]() 人,按上學所學時間分組如下:第
人,按上學所學時間分組如下:第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,第
,第![]() 組
組![]() ,得打如圖所示的頻率分布直方圖.
,得打如圖所示的頻率分布直方圖.
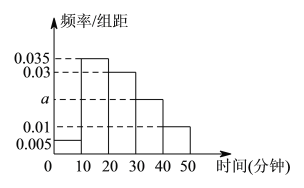
(Ⅰ)根據圖中數據求![]() 的值.
的值.
(Ⅱ)若從第![]() ,
,![]() ,
,![]() 組中用分成抽樣的方法抽取
組中用分成抽樣的方法抽取![]() 人參與交通安全問卷調查,應從這三組中各抽取幾人?
人參與交通安全問卷調查,應從這三組中各抽取幾人?
(Ⅲ)在(Ⅱ)的條件下,若從這![]() 人中隨機抽取
人中隨機抽取![]() 人參加交通安全宣傳活動,求第
人參加交通安全宣傳活動,求第![]() 組至少有
組至少有![]() 人被抽中的概率.
人被抽中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com