
【題目】汕頭某通訊設備廠為適應市場需求,提高效益,特投入98萬元引進世界先進設備奔騰6號,并馬上投入生產.第一年需要的各種費用是12萬元,從第二年開始,所需費用會比上一年增加4萬元,而每年因引入該設備可獲得的年利潤為50萬元.
請你根據以上數據,解決下列問題:(1)引進該設備多少年后,收回成本并開始盈利?(2)引進該設備若干年后,有兩種處理方案:第一種:年平均盈利達到最大值時,以26萬元的價格賣出;第二種:盈利總額達到最大值時,以8萬元的價格賣出.問哪種方案較為合算?并說明理由.
【答案】解:(1)設引進設備n年后開始盈利,盈利為y萬元,
則y=50n-(12n+![]() ×4)-98=-2n2+40n-98,由y>0,得10-
×4)-98=-2n2+40n-98,由y>0,得10-![]() <n<10+
<n<10+![]() .
.
∵n∈N*,∴3≤n≤17,即3年后開始盈利.…………………6分
(2)方案一:年平均盈利為![]() ,
,![]() =-2n-
=-2n-![]() +40≤-2
+40≤-2![]() +40=12,
+40=12,
當且僅當2n=![]() ,即n=7時,年平均利潤最大,共盈利12×7+26=110萬元.
,即n=7時,年平均利潤最大,共盈利12×7+26=110萬元.
方案二:盈利總額y=-2(n-10)2+102,n=10時,y取最大值102,
即經過10年盈利總額最大,
共計盈利102+8=110萬元.
兩種方案獲利相等,但由于方案二時間長,所以采用方案一合算.…………12分
【解析】
試題(1)根據利潤等于收入-成本,可求利潤函數,令其大于0,可得結論;
(2)分別求出兩種處理方案的利潤,再進行比較,即可得到結論.
試題解析:(1)設引進設備n年后開始盈利,盈利為y萬元,
則y=50n-(12n+![]() ×4)-98=-2n2+40n-98,
×4)-98=-2n2+40n-98,
由y>0,得10-![]() <n<10+
<n<10+![]() .
.
∵n∈N*,∴3≤n≤17,即3年后開始盈利.
(2)方案一:年平均盈利為![]() ,
,![]() =-2n-
=-2n-![]() +40≤-2
+40≤-2![]() +40=12,
+40=12,
當且僅當2n=![]() ,即n=7時,年平均利潤最大,共盈利12×7+26=110萬元.
,即n=7時,年平均利潤最大,共盈利12×7+26=110萬元.
方案二:盈利總額y=-2(n-10)2+102,n=10時,y取最大值102,
即經過10年盈利總額最大, 共計盈利102+8=110萬元.
兩種方案獲利相等,但由于方案二時間長,所以采用方案一合算.


 開心蛙狀元測試卷系列答案
開心蛙狀元測試卷系列答案科目:高中數學 來源: 題型:
【題目】執行兩次如圖所示的程序框圖,若第一次輸入的x值為7,第二次輸入的x值為9,則第一次,第二次輸出的a值分別為( )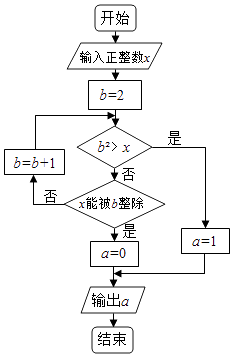
A.0,0
B.1,1
C.0,1
D.1,0
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,曲線C1的極坐標方程為ρcosθ=4.
(Ⅰ)M為曲線C1上的動點,點P在線段OM上,且滿足|OM||OP|=16,求點P的軌跡C2的直角坐標方程;
(Ⅱ)設點A的極坐標為(2, ![]() ),點B在曲線C2上,求△OAB面積的最大值.
),點B在曲線C2上,求△OAB面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合![]() 是滿足下列條件的函數
是滿足下列條件的函數![]() 的全體:在定義域內存在實數
的全體:在定義域內存在實數![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)判斷冪函數![]() 是否屬于集合
是否屬于集合![]() ?并說明理由;
?并說明理由;
(Ⅱ)設![]() ,
, ![]() ,
,
i)當![]() 時,若
時,若![]() ,求
,求![]() 的取值范圍;
的取值范圍;
ii)若對任意的![]() ,都有
,都有![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(12分)為考察某種藥物預防疾病的效果,進行動物試驗,調查了105個樣本,統計結果為:服藥的共有55個樣本,服藥但患病的仍有10個樣本,沒有服藥且未患病的有30個樣本.
(1)根據所給樣本數據完成2×2列聯表中的數據;
(2)請問能有多大把握認為藥物有效?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市計劃按月訂購一種酸奶,每天進貨量相同,進貨成本每瓶4元,售價每瓶6元,未售出的酸奶降價處理,以每瓶2元的價格當天全部處理完.根據往年銷售經驗,每天需求量與當天最高氣溫(單位:℃)有關.如果最高氣溫不低于25,需求量為500瓶;如果最高氣溫位于區間[20,25),需求量為300瓶;如果最高氣溫低于20,需求量為200瓶.為了確定六月份的訂購計劃,統計了前三年六月份各天的最高氣溫數據,得下面的頻數分布表:
最高氣溫 | [10,15) | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) |
天數 | 2 | 16 | 36 | 25 | 7 | 4 |
以最高氣溫位于各區間的頻率代替最高氣溫位于該區間的概率.
(Ⅰ)求六月份這種酸奶一天的需求量X(單位:瓶)的分布列;
(Ⅱ)設六月份一天銷售這種酸奶的利潤為Y(單位:元),當六月份這種酸奶一天的進貨量n(單位:瓶)為多少時,Y的數學期望達到最大值?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線C的參數方程是 ![]() (θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,A、B的極坐標分別為A﹣(2,0)、B(﹣1,
(θ為參數),以坐標原點為極點,x軸的正半軸為極軸建立極坐標系,A、B的極坐標分別為A﹣(2,0)、B(﹣1, ![]() )
)
(1)求直線AB的直角坐標方程;
(2)在曲線C上求一點M,使點M到AB的距離最大,并求出些最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com