
【題目】已知![]() ,函數(shù)
,函數(shù)![]() .
.
(1)若![]() ,證明:函數(shù)
,證明:函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù);
上是單調(diào)增函數(shù);
(2)求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值;
上的最大值;
(3)若函數(shù)![]() 的圖像過原點(diǎn),且
的圖像過原點(diǎn),且![]() 的導(dǎo)數(shù)
的導(dǎo)數(shù)![]() ,當(dāng)
,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 過點(diǎn)
過點(diǎn)![]() 的切線至少有2條,求實(shí)數(shù)
的切線至少有2條,求實(shí)數(shù)![]() 的值.
的值.
【答案】(1)證明見解析;(2)當(dāng)![]() 時,最大值為
時,最大值為![]() ;當(dāng)
;當(dāng)![]() 時,最大值為
時,最大值為![]() (3)
(3)![]()
【解析】
(1)由題![]() ,利用導(dǎo)函數(shù)求單調(diào)區(qū)間即可;
,利用導(dǎo)函數(shù)求單調(diào)區(qū)間即可;
(2)利用導(dǎo)數(shù)可以推導(dǎo)得到![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在區(qū)間
上是減函數(shù),在區(qū)間![]() 上是增函數(shù),則當(dāng)
上是增函數(shù),則當(dāng)![]() 時,
時,![]() 的最大值為
的最大值為![]() 和
和![]() 中的最大值,作差可得
中的最大值,作差可得![]() ,設(shè)
,設(shè)![]() ,再次利用導(dǎo)數(shù)推導(dǎo)
,再次利用導(dǎo)數(shù)推導(dǎo)![]() 的單調(diào)性,進(jìn)而得到
的單調(diào)性,進(jìn)而得到![]() 上的最大值;
上的最大值;
(3)由題可得![]() ,設(shè)切點(diǎn)為
,設(shè)切點(diǎn)為![]() ,則
,則![]() 處的切線方程為:
處的切線方程為:![]() ,將
,將![]() 代入可得
代入可得![]() ,則將原命題等價為關(guān)于
,則將原命題等價為關(guān)于![]() 的方程至少有2個不同的解,設(shè)
的方程至少有2個不同的解,設(shè)![]() ,進(jìn)而利用導(dǎo)函數(shù)判斷
,進(jìn)而利用導(dǎo)函數(shù)判斷![]() 的單調(diào)性,從而求解即可
的單調(diào)性,從而求解即可
(1)證明:![]() ,則
,則![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,
時,![]() ,
,
![]()
![]() ,即此時函數(shù)
,即此時函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù).
上是單調(diào)增函數(shù).
(2)由(1)知,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù),
上是單調(diào)增函數(shù),
當(dāng)![]() 時,
時,![]() ,則
,則![]() ,
,![]() ,則
,則![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)減函數(shù);
上是單調(diào)減函數(shù);
同理,當(dāng)![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)增函數(shù),在區(qū)間
上是單調(diào)增函數(shù),在區(qū)間![]() 上是單調(diào)減函數(shù);
上是單調(diào)減函數(shù);
即當(dāng)![]() ,且
,且![]() 時,
時,![]() 在區(qū)間
在區(qū)間![]() 上是減函數(shù),在區(qū)間
上是減函數(shù),在區(qū)間![]() 上是增函數(shù),
上是增函數(shù),
則當(dāng)![]() 時,
時,![]() 的最大值為
的最大值為![]() 和
和![]() 中的最大值,
中的最大值,
![]() ,
,
![]() 令
令![]() ,
,
則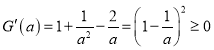 ,
,
![]()
![]() 在
在![]() 上為增函數(shù),
上為增函數(shù),
![]() ,
,
![]() 當(dāng)
當(dāng)![]() 時,
時,![]() ,即
,即![]() ,此時最大值為
,此時最大值為![]() ;
;
當(dāng)![]() 時,
時,![]() ,即
,即![]() ,此時最大值為
,此時最大值為![]() .
.
(3)![]()
![]() ,
,
![]()
![]() ,
,
![]()
![]() 的圖像過原點(diǎn),
的圖像過原點(diǎn),
![]() ,即
,即![]() ,則
,則![]() ,
,
設(shè)切點(diǎn)為![]() ,則
,則![]() 處的切線方程為:
處的切線方程為:![]() ,
,
將![]() 代入得
代入得![]() ,
,
即![]() (※),
(※),
則原命題等價為關(guān)于![]() 的方程(※)至少有2個不同的解,
的方程(※)至少有2個不同的解,
設(shè)![]() ,
,
則![]() ,
,
令![]() ,
,![]() ,
,
![]() ,
,
當(dāng)![]() 和
和![]() 時,
時,![]() ,此時函數(shù)
,此時函數(shù)![]() 為增函數(shù);
為增函數(shù);
當(dāng)![]() 時,
時,![]() ,此時函數(shù)
,此時函數(shù)![]() 減函數(shù),
減函數(shù),
![]()
![]() 的極大值為
的極大值為![]() ,
,
![]() 的極小值為
的極小值為![]() ,
,
設(shè)![]() ,則
,則![]() ,則原命題等價為
,則原命題等價為![]() ,即
,即![]() 對
對![]() 恒成立,
恒成立,
![]() 由
由![]() 得
得![]() ,
,
設(shè)![]() ,則
,則![]() ,
,
令![]() ,則
,則![]() ,
,![]() ,當(dāng)
,當(dāng)![]() 時,
時,![]() ;當(dāng)
;當(dāng)![]() 時,
時,![]() ,
,
即![]() 在
在![]() 上單調(diào)遞增,在
上單調(diào)遞增,在![]() 上單調(diào)遞減,
上單調(diào)遞減,
![]() 的最大值為
的最大值為![]() ,
,![]()
![]() ,
,
故![]() ,
,
綜上所述,當(dāng)![]() 時,函數(shù)
時,函數(shù)![]() 過點(diǎn)
過點(diǎn)![]() 的切線至少有2條,此時實(shí)數(shù)m的值為
的切線至少有2條,此時實(shí)數(shù)m的值為![]()



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】2018年遼寧省正式實(shí)施高考改革.新高考模式下,學(xué)生將根據(jù)自己的興趣、愛好、學(xué)科特長和高校提供的“選考科目要求”進(jìn)行選課.這樣學(xué)生既能尊重自己愛好、特長做好生涯規(guī)劃,又能發(fā)揮學(xué)科優(yōu)勢,進(jìn)而在高考中獲得更好的成績和實(shí)現(xiàn)自己的理想.考改實(shí)施后,學(xué)生將在高二年級將面臨著![]() 的選課模式,其中“3”是指語、數(shù)、外三科必學(xué)內(nèi)容,“1”是指在物理和歷史中選擇一科學(xué)習(xí),“2”是指在化學(xué)、生物、地理、政治四科中任選兩科學(xué)習(xí).某校為了更好的了解學(xué)生對“1”的選課情況,學(xué)校抽取了部分學(xué)生對選課意愿進(jìn)行調(diào)查,依據(jù)調(diào)查結(jié)果制作出如下兩個等高堆積條形圖:根據(jù)這兩幅圖中的信息,下列哪個統(tǒng)計結(jié)論是不正確的( )
的選課模式,其中“3”是指語、數(shù)、外三科必學(xué)內(nèi)容,“1”是指在物理和歷史中選擇一科學(xué)習(xí),“2”是指在化學(xué)、生物、地理、政治四科中任選兩科學(xué)習(xí).某校為了更好的了解學(xué)生對“1”的選課情況,學(xué)校抽取了部分學(xué)生對選課意愿進(jìn)行調(diào)查,依據(jù)調(diào)查結(jié)果制作出如下兩個等高堆積條形圖:根據(jù)這兩幅圖中的信息,下列哪個統(tǒng)計結(jié)論是不正確的( )
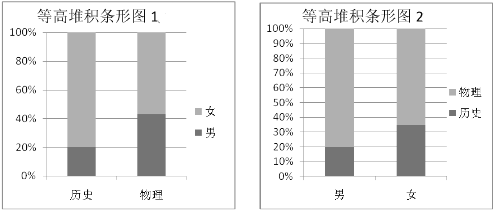
A.樣本中的女生數(shù)量多于男生數(shù)量
B.樣本中有學(xué)物理意愿的學(xué)生數(shù)量多于有學(xué)歷史意愿的學(xué)生數(shù)量
C.樣本中的男生偏愛物理
D.樣本中的女生偏愛歷史
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】數(shù)列![]() 各項均不為0,前n項和為
各項均不為0,前n項和為![]() ,
,![]() ,
,![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)若數(shù)列![]() 共3項,求所有滿足要求的數(shù)列;
共3項,求所有滿足要求的數(shù)列;
(2)求證:![]() 是滿足已知條件的一個數(shù)列;
是滿足已知條件的一個數(shù)列;
(3)請構(gòu)造出一個滿足已知條件的無窮數(shù)列![]() ,并使得
,并使得![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() 的中心在坐標(biāo)原點(diǎn),且經(jīng)過點(diǎn)
的中心在坐標(biāo)原點(diǎn),且經(jīng)過點(diǎn)![]() ,它的一個焦點(diǎn)與拋物線
,它的一個焦點(diǎn)與拋物線![]() 的焦點(diǎn)重合.
的焦點(diǎn)重合.
(1)求橢圓![]() 的方程;
的方程;
(2)斜率為![]() 的直線過點(diǎn)
的直線過點(diǎn)![]() ,且與拋物線
,且與拋物線![]() 交于
交于![]() 兩點(diǎn),設(shè)點(diǎn)
兩點(diǎn),設(shè)點(diǎn)![]() ,
,![]() 的面積為
的面積為![]() ,求
,求![]() 的值;
的值;
(3)若直線![]() 過點(diǎn)
過點(diǎn)![]()
![]() ,且與橢圓
,且與橢圓![]() 交于
交于![]() 兩點(diǎn),點(diǎn)
兩點(diǎn),點(diǎn)![]() 關(guān)于
關(guān)于![]() 軸的對稱點(diǎn)為
軸的對稱點(diǎn)為![]() ,直線
,直線![]() 的縱截距為
的縱截距為![]() ,證明:
,證明:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】下列命題是真命題的是( )
A.有兩個面相互平行,其余各面都是平行四邊形的多面體是棱柱
B.正四面體是四棱錐
C.有一個面是多邊形,其余各面都是三角形的多面體叫做棱錐
D.正四棱柱是平行六面體
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】甲、乙、丙三家企業(yè)產(chǎn)品的成本分別為10000,12000,15000,其成本構(gòu)成如下圖所示,則關(guān)于這三家企業(yè)下列說法錯誤的是( )
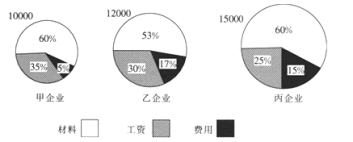
A.成本最大的企業(yè)是丙企業(yè)B.費(fèi)用支出最高的企業(yè)是丙企業(yè)
C.支付工資最少的企業(yè)是乙企業(yè)D.材料成本最高的企業(yè)是丙企業(yè)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】李克強(qiáng)總理在很多重大場合都提出“大眾創(chuàng)業(yè),萬眾創(chuàng)新”.某創(chuàng)客,白手起家,2015年一月初向銀行貸款十萬元做創(chuàng)業(yè)資金,每月獲得的利潤是該月初投入資金的![]() .每月月底需要交納房租和所得稅共為該月全部金額(包括本金和利潤)的
.每月月底需要交納房租和所得稅共為該月全部金額(包括本金和利潤)的![]() ,每月的生活費(fèi)等開支為3000元,余款全部投入創(chuàng)業(yè)再經(jīng)營.如此每月循環(huán)繼續(xù).
,每月的生活費(fèi)等開支為3000元,余款全部投入創(chuàng)業(yè)再經(jīng)營.如此每月循環(huán)繼續(xù).
(1)問到2015年年底(按照12個月計算),該創(chuàng)客有余款多少元?(結(jié)果保留至整數(shù)元)
(2)如果銀行貸款的年利率為![]() ,問該創(chuàng)客一年(12個月)能否還清銀行貸款?
,問該創(chuàng)客一年(12個月)能否還清銀行貸款?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某地擬建造一座大型體育館,其設(shè)計方案側(cè)面的外輪廓如圖所示,曲線![]() 是以點(diǎn)
是以點(diǎn)![]() 為圓心的圓的一部分,其中
為圓心的圓的一部分,其中![]() ;曲線
;曲線![]() 是拋物線
是拋物線![]() 的一部分;
的一部分;![]() ,且
,且![]() 恰好等于圓
恰好等于圓![]() 的半徑.假定擬建體育館的高
的半徑.假定擬建體育館的高![]() (單位:米,下同).
(單位:米,下同).
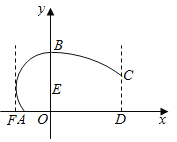
(1)若![]() ,
,![]() ,求
,求![]() 、
、![]() 的長度;
的長度;
(2)若要求體育館側(cè)面的最大寬度![]() 不超過
不超過![]() 米,求
米,求![]() 的取值范圍;
的取值范圍;
(3)若![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】所謂聲強(qiáng),是指聲音在傳播途徑上每1平方米面積上的聲能流密度,用I表示,人類能聽到的聲強(qiáng)范圍很廣,其中能聽見的1000Hz聲音的聲強(qiáng)(約10﹣12W/m2)為標(biāo)準(zhǔn)聲強(qiáng),記作I0,聲強(qiáng)I與標(biāo)準(zhǔn)聲強(qiáng)I0之比的常用對數(shù)稱作聲強(qiáng)的聲強(qiáng)級,記作L,即L=lg![]() ,聲強(qiáng)級L的單位名稱為貝(爾),符號為B,取貝(爾)的十分之一作為響度的常用單位,稱為分貝(爾).簡稱分貝(dB).《三國演義》中有張飛喝斷當(dāng)陽橋的故事,設(shè)張飛大喝一聲的響度為140dB.一個士兵大喝一聲的響度為90dB,如果一群士兵同時大喝一聲相當(dāng)一張飛大喝一聲的響度,那么這群土兵的人數(shù)為( )
,聲強(qiáng)級L的單位名稱為貝(爾),符號為B,取貝(爾)的十分之一作為響度的常用單位,稱為分貝(爾).簡稱分貝(dB).《三國演義》中有張飛喝斷當(dāng)陽橋的故事,設(shè)張飛大喝一聲的響度為140dB.一個士兵大喝一聲的響度為90dB,如果一群士兵同時大喝一聲相當(dāng)一張飛大喝一聲的響度,那么這群土兵的人數(shù)為( )
A.1萬B.2萬C.5萬D.10萬
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com