
分析 (1)列方程組計算a,b得出f(x);
(2)計算x1,x2,x3,根據前三項猜想通項公式,并用數學歸納法證明.
解答 解:(1)∵f(1)=$\frac{1}{4}$,f(-2)=1,
∴$\left\{\begin{array}{l}{\frac{b+1}{(a+1)^{2}}=\frac{1}{4}}\\{\frac{-2b+1}{(-2a+1)^{2}}=1}\end{array}\right.$,又a>0,解得a=1,b=0.
∴f(x)=$\frac{1}{(x+1)^{2}}$.
(2)x1=1-f(1)=1-$\frac{1}{4}$=$\frac{3}{4}$;
x2=(1-f(1))(1-f(2))=$\frac{3}{4}×$$\frac{8}{9}$=$\frac{2}{3}$,
x3=(1-f(1))(1-f(2))(1-f(3))=$\frac{5}{8}$,
猜想:xn=$\frac{n+2}{2n+2}$.
證明:①當n=1時,猜想顯然成立,
②假設n=k(k≥1)時猜想成立,即xk=$\frac{k+2}{2k+2}$.
則xk+1=xk(1-f(k+1))=$\frac{k+2}{2k+2}$•(1-$\frac{1}{(k+2)^{2}}$)=$\frac{k+2}{2k+2}•$$\frac{(k+1)(k+3)}{(k+2)^{2}}$=$\frac{k+3}{2(k+2)}$=$\frac{k+1+2}{2(k+1)+2}$.
∴當n=k+1時,猜想成立.
∴對任意n∈N+,都有xn=$\frac{n+2}{2n+2}$.
點評 本題考查了待定系數法求解析式,數學歸納法證明,屬于中檔題.


科目:高中數學 來源: 題型:解答題
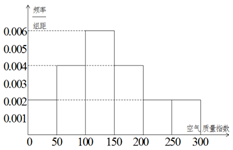 某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如表(假設該區域空氣質量指數不會超過300):
某中學的環保社團參照國家環境標準制定了該校所在區域空氣質量指數與空氣質量等級對應關系如表(假設該區域空氣質量指數不會超過300):| 空氣質量指數 | (0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] |
| 空氣質量等級 | 1級優 | 2級良 | 3級輕度 污染 | 4級中度 污染 | 5級重度 污染 | 6級嚴重污染 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 上網時間(分鐘) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人數 | 5 | 25 | 30 | 25 | 15 |
| 上網時間(分鐘) | [30,40) | [40,50) | [50,60) | [60,70) | [70,80] |
| 人數 | 10 | 20 | 40 | 20 | 10 |
| 上網時間少于60分鐘 | 上網時間不少于60分鐘 | 合計 | |
| 男生 | 60 | 40 | 100 |
| 女生 | 70 | 30 | 100 |
| 合計 | 130 | 70 | 200 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 向左平移$\frac{π}{6}$個單位長度 | B. | 向右平移$\frac{π}{6}$個單位長度 | ||
| C. | 向左平移$\frac{π}{3}$個單位長度 | D. | 向右平移$\frac{π}{3}$個單位長度 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com