【題目】若直線
與曲線
滿足下列兩個條件：
（i)直線
在點
處與曲線
相切；（ii)曲線
在點
附近位于直線
的兩側.則稱直線
在點
處“切過”曲線
.
下列命題正確的是__________(寫出所有正確命題的編號).
①直線
在點
處“切過”曲線
；
②直線
在點
處“切過”曲線
；
③直線
在點
處“切過”曲線
；
④直線
在點
處“切過”曲線
；
⑤直線
在點
處“切過”曲線
.
輕松奪冠全能掌控卷系列答案科目：高中數學 來源： 題型：
【題目】邗江中學高二年級某班某小組共10人，利用寒假參加義工活動，已知參加義工活動次數為1，2，3的人數分別為3，3，4．現從這10人中選出2人作為該組代表參加座談會．
（1）記“選出2人參加義工活動的次數之和為4”為事件
，求事件發生的概率；
（2）設
為選出2人參加義工活動次數之差的絕對值，求隨機變量的分布列和數學期望．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】把長
和寬
分別為
和2的長方形
沿對角線
折成
的二面角
，下列正確的命題序號是__________．
①四面體外接球的體積隨
的改變而改變；
②
的長度隨的增大而增大；
③當
時，長度最長；
④當
時，長度等于
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】【2018屆北京市海淀區】如圖，三棱柱
側面
底面
， 
， 
分別為棱
的中點.
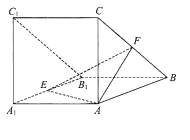
（Ⅰ）求證： 
；
（Ⅱ）求三棱柱
的體積；
（Ⅲ）在直線
上是否存在一點
，使得
平面
？若存在，求出
的長；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】無窮數列
滿足： 
為正整數，且對任意正整數
， 
為前
項
， 
， 
， 
中等于
的項的個數.
（Ⅰ）若
，請寫出數列
的前7項；
（Ⅱ）求證：對于任意正整數
，必存在
，使得
；
（Ⅲ）求證:“
”是“存在
，當
時，恒有
成立”的充要條件。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2017·太原三模)已知等比數列{an}的各項均為不等于1的正數，數列{bn}滿足bn＝lgan，b3＝18，b6＝12，則數列{bn}的前n項和的最大值為( )
A. 126 B. 130 C. 132 D. 134
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖矩形
中， 
.點
在
邊上， 
且
， 
沿直線
向上折起成
．記二面角
的平面角為
，當
時，
①存在某個位置，使
；
②存在某個位置，使
；
③任意兩個位置，直線
和直線
所成的角都不相等.
以上三個結論中正確的序號是
A. ① B. ①② C. ①③ D. ②③
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
