
在極坐標系中,已知點P為圓ρ2+2ρsinθ﹣7=0上任一點.求點P到直線ρcosθ+ρsinθ﹣7=0的距離的最小值與最大值.
dmin=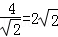 ,dmax=
,dmax=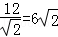
解析試題分析:由題意圓的普通方程為 x2+y2+2y﹣7=0,參數方程為 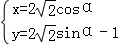 (α為參數),直線的極坐標方程為ρcosθ+ρsinθ﹣7=0.將圓和直線先化為一般方程坐標,然后再計算橢圓上點到直線距離的最大值和最小值即可.
(α為參數),直線的極坐標方程為ρcosθ+ρsinθ﹣7=0.將圓和直線先化為一般方程坐標,然后再計算橢圓上點到直線距離的最大值和最小值即可.
圓ρ2+2ρsinθ﹣7=0的普通方程為 x2+y2+2y﹣7=0,…(2分)
直線ρcosθ+ρsinθ﹣7=0的普通方程為x+y﹣7=0,…(4分)
設點P(2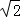 cosα,2
cosα,2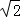 sinα﹣1),
sinα﹣1),
則點P到直線x+y﹣7=0的距離
d=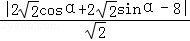 =
=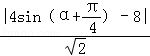 …(8分)
…(8分)
所以dmin=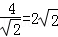 ,
,
dmax=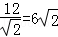 .…(10分)
.…(10分)
考點:點的極坐標和直角坐標的互化;直線與圓的位置關系
點評:此題考查參數方程、極坐標方程與普通方程的區別和聯系,兩者要會互相轉化,根據實際情況選擇不同的方程進行求解,這也是每年高考必考的熱點問題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
在直角坐標系中,曲線C的參數方程為 (
( 為參數).以原點為極點,x軸的正半軸為極軸建立極坐標系,點
為參數).以原點為極點,x軸的正半軸為極軸建立極坐標系,點 ,直線
,直線 的極坐標方程為
的極坐標方程為 .
.
(1)判斷點 與直線
與直線 的位置關系,說明理由;
的位置關系,說明理由;
(2)設直線 與曲線C的兩個交點為A、B,求
與曲線C的兩個交點為A、B,求 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線 過點P(-2,-4)的直線
過點P(-2,-4)的直線 為參數)與曲線C相交于點M,N兩點.
為參數)與曲線C相交于點M,N兩點.
(Ⅰ)求曲線C和直線 的普通方程;
的普通方程;
(Ⅱ)若|PM|,|MN|,|PN |成等比數列,求實數a的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在平面直角坐標系xOy中,曲線C1的參數方程為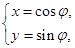 (
(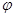 為參數)曲線C2的參數方程為
為參數)曲線C2的參數方程為 (
(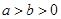 ,
,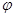 為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=
為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ= 與C1,C2各有一個交點.當
與C1,C2各有一個交點.當 =0時,這兩個交點間的距離為2,當
=0時,這兩個交點間的距離為2,當 =
=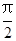 時,這兩個交點重合.
時,這兩個交點重合.
(I)分別說明C1,C2是什么曲線,并求出a與b的值;
(II)設當 =
= 時,l與C1,C2的交點分別為A1,B1,當
時,l與C1,C2的交點分別為A1,B1,當 =-
=- 時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在平面直角坐標系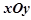 中,曲線
中,曲線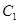 為
為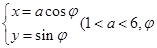 為參數)。在以
為參數)。在以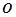 為原點,
為原點,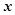 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線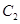 的極坐標方程為
的極坐標方程為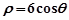 ,射線為
,射線為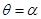 ,與
,與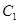 的交點為
的交點為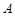 ,與
,與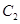 除極點外的一個交點為
除極點外的一個交點為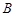 。當
。當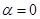 時,
時,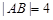 。
。
(1)求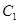 ,
,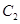 的直角坐標方程;
的直角坐標方程;
(2)設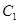 與
與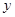 軸正半軸交點為
軸正半軸交點為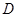 ,當
,當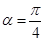 時,設直線
時,設直線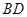 與曲線
與曲線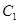 的另一個交點為
的另一個交點為 ,求
,求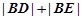 。
。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知曲線C的極坐標方程 是 =1,以極點為原點,極軸為
=1,以極點為原點,極軸為 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線 的參數方程為
的參數方程為 為參數)。
為參數)。
(1)寫出直線 與曲線C的直角坐標方程;
與曲線C的直角坐標方程;
(2)設曲線C經過伸縮變換 得到曲線
得到曲線 ,設曲線
,設曲線 上任一點為
上任一點為 ,求
,求 的最小值。
的最小值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本題滿分10分) 在直角坐標系 中,以
中,以 極點,
極點, 軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為 分別為
分別為 與
與 軸,
軸, 軸的交點
軸的交點
(1)寫出 的直角坐標方程,并求出
的直角坐標方程,并求出 的極坐標
的極坐標
(2)設 的中點為
的中點為 ,求直線
,求直線 的極坐標方程
的極坐標方程
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com