
在平面直角坐標系xOy中,曲線C1的參數方程為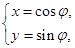 (
(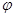 為參數)曲線C2的參數方程為
為參數)曲線C2的參數方程為 (
(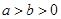 ,
,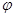 為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=
為參數)在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ= 與C1,C2各有一個交點.當
與C1,C2各有一個交點.當 =0時,這兩個交點間的距離為2,當
=0時,這兩個交點間的距離為2,當 =
=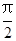 時,這兩個交點重合.
時,這兩個交點重合.
(I)分別說明C1,C2是什么曲線,并求出a與b的值;
(II)設當 =
= 時,l與C1,C2的交點分別為A1,B1,當
時,l與C1,C2的交點分別為A1,B1,當 =-
=- 時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.
(1)a=3,b=1。
(2)四邊形 的面積為
的面積為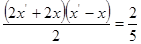
解析試題分析:(1)C1是圓,C2是橢圓
當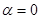 時,射線l與C1,C2的交點的直角坐標分別是(1,0)(a,0),因為兩點間的距離為2,所以a=3
時,射線l與C1,C2的交點的直角坐標分別是(1,0)(a,0),因為兩點間的距離為2,所以a=3
當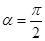 時,射線l與C1,C2的交點的直角坐標分別是(0,1)(0,b),因為兩點重合,所以b=1
時,射線l與C1,C2的交點的直角坐標分別是(0,1)(0,b),因為兩點重合,所以b=1
(2)C1,C2的普通方程為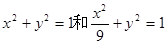

當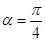 時,射線l與C1的交點
時,射線l與C1的交點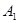 的橫坐標為
的橫坐標為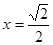 ,與
,與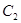 的交點
的交點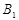 的橫坐標為
的橫坐標為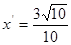
當 時,射線l與C1,C2的兩個交點
時,射線l與C1,C2的兩個交點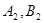 分別與
分別與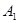 ,
,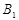 關于x軸對稱,因此四邊形
關于x軸對稱,因此四邊形 為梯形。故四邊形
為梯形。故四邊形 的面積為
的面積為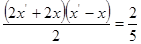
考點:極坐標方程、參數方程與直角坐標方程的互化,面積計算。
點評:中檔題,利用極坐標、直角坐標轉化公式。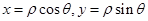 。參數方程化為普通方程,常用的“消參”方法有,代入消參、加減消參、平方關系消參等。確定四邊形的面積,要注意發現其幾何特征,探尋計算方法。
。參數方程化為普通方程,常用的“消參”方法有,代入消參、加減消參、平方關系消參等。確定四邊形的面積,要注意發現其幾何特征,探尋計算方法。


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:高中數學 來源: 題型:解答題
已知曲線 的極坐標方程是
的極坐標方程是 ,直線的參數方程是
,直線的參數方程是 (為參數).
(為參數).
(Ⅰ)將曲線 的極坐標方程化為直角坐標方程;
的極坐標方程化為直角坐標方程;
(Ⅱ)設直線與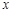 軸的交點是
軸的交點是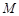 ,
, 是曲線
是曲線 上一動點,求
上一動點,求 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分10分)選修4-4:坐標系與參數方程
已知直線的極坐標方程為 ,圓
,圓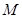 的參數方程為
的參數方程為 (其中
(其中 為參數).
為參數).
(Ⅰ)將直線的極坐標方程化為直角坐標方程;
(Ⅱ)求圓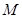 上的點到直線的距離的最小值.
上的點到直線的距離的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在極坐標系中,圓C的方程為ρ=2  sin
sin  ,以極點為坐標原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為
,以極點為坐標原點,極軸為x軸的正半軸建立平面直角坐標系,直線l的參數方程為 (t為參數),判斷直線l和圓C的位置關系.
(t為參數),判斷直線l和圓C的位置關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com