
【題目】已知函數![]() ,
, ![]()
![]() .
.
(Ⅰ)若直線![]()
![]() 與曲線
與曲線![]() 和
和![]() 分別交于
分別交于![]() 兩點.設曲線
兩點.設曲線
![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
, ![]() 在點
在點![]() 處的切線為
處的切線為![]() .
.
(ⅰ)當![]() 時,若
時,若![]()
![]() ,求
,求![]() 的值;
的值;
(ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)設函數![]() 在其定義域內恰有兩個不同的極值點
在其定義域內恰有兩個不同的極值點![]() ,
, ![]() ,且
,且![]() .
.
若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
【答案】(1)(ⅰ)![]() (ⅱ)
(ⅱ) ![]() (2)
(2)![]()
【解析】試題分析:(1)由![]() 和導數可得
和導數可得![]() ,
, ![]() ,可求得
,可求得![]() 。
。
由![]() ,則
,則![]() 在
在![]() 上有解. 即
上有解. 即![]() 在
在![]() 上有解.
上有解.
設![]() ,
, ![]() ,則
,則![]() .分
.分![]() ,a=0,a>0討論。(2)
,a=0,a>0討論。(2)
![]() .
. ![]() 在其定義域內的兩個不同的極值點
在其定義域內的兩個不同的極值點![]() ,. 即
,. 即![]() ,
, ![]() . 兩式作差得,
. 兩式作差得, ![]() . 由
. 由![]()
![]()
![]()
![]() . 令
. 令![]() ,則
,則![]() ,由題意知: l
,由題意知: l![]()
![]() 在
在![]() 上恒成立, 可求
上恒成立, 可求![]() 范圍。
范圍。
試題解析: (Ⅰ) 函數![]() 的定義域為
的定義域為![]() .
.
![]() ,
, ![]() .
.
(ⅰ)當![]() 時,
時, ![]() ,
, ![]() .
.
因為![]() ,所以
,所以![]() . 即
. 即![]() .
.
解得![]() .
.
(ⅱ)因為![]() ,則
,則![]() 在
在![]() 上有解. 即
上有解. 即![]() 在
在![]() 上有解.
上有解.
設![]() ,
, ![]() ,則
,則![]() .
.
當![]() 時,
時, ![]() 恒成立,則函數
恒成立,則函數![]() 在
在![]() 上為增函數.
上為增函數.
![]() 當
當![]() 時,取
時,取![]() ,
, ![]()
取![]() ,
, ![]() , 所以
, 所以![]() 在
在![]() 上存在零點.
上存在零點.
![]() 當
當![]() 時,
時, ![]() 存在零點,
存在零點, ![]() ,滿足題意.
,滿足題意.
(2)當![]() 時,令
時,令![]() ,則
,則![]() .則
.則![]() 在
在![]() 上為增函數,
上為增函數, ![]() 上為減函數.
上為減函數.
所以![]() 的最大值為
的最大值為![]() .解得
.解得![]() .
.
取![]() ,
, ![]() .
.
因此當![]() 時,方程
時,方程![]() 在
在![]() 上有解.
上有解.
所以, ![]() 的最大值是
的最大值是![]() .
.
另解:函數![]() 的定義域為
的定義域為![]() .
. ![]() ,
, ![]() .
.
則![]() ,
, ![]() .
.
因為![]() ,則
,則![]() 在
在![]() 上有解.即
上有解.即![]() 在
在![]() 上有解.
上有解.
因為![]() ,所以
,所以![]() .
.
令![]() (
(![]() ).
).![]() .得
.得![]() .
.
當![]() ,
, ![]() ,
, ![]() 為增函數;
為增函數;
當![]() ,
, ![]() ,
, ![]() 為減函數;
為減函數;
所以![]() .
.
所以, ![]() 的最大值是
的最大值是![]() .
.
(Ⅱ) ![]()
![]()
![]() .
.
因為![]() 為
為![]() 在其定義域內的兩個不同的極值點,
在其定義域內的兩個不同的極值點,
所以![]() 是方程
是方程![]() 的兩個根. 即
的兩個根. 即![]() ,
, ![]() .
.
兩式作差得, ![]() .
.
因為![]()
![]() ,由
,由![]() ,得
,得![]() . 則
. 則![]()
![]()
![]()
![]() . 令
. 令![]() ,則
,則![]() ,由題意知:
,由題意知:
![]()
![]() 在
在![]() 上恒成立,
上恒成立,
令![]() ,
,
則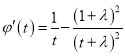 =
=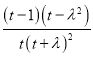 .當
.當![]() ,即
,即![]() 時,
時, ![]() ,
, ![]() ,
,
所以![]() 在
在![]() 上單調遞增.
上單調遞增.
又![]() ,則
,則![]() 在
在![]() 上恒成立.
上恒成立.
當![]() ,即
,即![]() 時,
時, ![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為增函數; 當
上為增函數; 當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 上為減函數.
上為減函數.
又![]() ,所以
,所以![]() 不恒小于
不恒小于![]() ,不合題意.
,不合題意.
綜上, ![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=﹣x3+ax在(﹣1,0)上是增函數.
(1)求實數a的取值范圍A;
(2)當a為A中最小值時,定義數列{an}滿足:a1∈(﹣1,0),且2an+1=f(an),用數學歸納法證明an∈(﹣1,0),并判斷an+1與an的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司為感謝全體員工的辛勤勞動,決定在年終答謝會上,通過摸球方式對全公司1000位員工進行現金抽獎。規定:每位員工從裝有4個相同質地球的袋子中一次性隨機摸出2個球,這4個球上分別標有數字![]() 、
、![]() 、
、![]() 、
、![]() ,摸出來的兩個球上的數字之和為該員工所獲的獎勵額
,摸出來的兩個球上的數字之和為該員工所獲的獎勵額![]() (單位:元)。公司擬定了以下三個數字方案:
(單位:元)。公司擬定了以下三個數字方案:
方案 |
|
|
|
|
一 | 100 | 100 | 100 | 500 |
二 | 100 | 100 | 500 | 500 |
三 | 200 | 200 | 400 | 400 |
(Ⅰ)如果采取方案一,求![]() 的概率;
的概率;
(Ⅱ)分別計算方案二、方案三的平均數![]() 和方差
和方差![]() ,如果要求員工所獲的獎勵額相對均衡,方案二和方案三選擇哪個更好?
,如果要求員工所獲的獎勵額相對均衡,方案二和方案三選擇哪個更好?
(Ⅲ)在投票選擇方案二還是方案三時,公司按性別分層抽取100名員工進行統計,得到如下不完整的![]() 列聯表。請將該表補充完整,并判斷能否有90%的把握認為“選擇方案二或方案三與性別有關”?
列聯表。請將該表補充完整,并判斷能否有90%的把握認為“選擇方案二或方案三與性別有關”?
方案二 | 方案三 | 合計 | |
男性 | 12 | ||
女性 | 40 | ||
合計 | 82 | 100 |
附:![]()
| 0.15 | 0.10 | 0.05 |
| 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設定義在R上的偶函數f(x),滿足對任意x∈R都有f(t)=f(2﹣t)且x∈(0,1]時,f(x)= ![]() ,a=f(
,a=f( ![]() ),b=f(
),b=f( ![]() ),c=f(
),c=f( ![]() ),用“<“表示a,b,c的大小關系是 .
),用“<“表示a,b,c的大小關系是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】富華中學的一個文學興趣小組中,三位同學張博源、高家銘和劉雨恒分別從莎士比亞、雨果和曹雪芹三位名家中選擇了一位進行性格研究,并且他們選擇的名家各不相同.三位同學一起來找圖書管理員劉老師,讓劉老師猜猜他們三人各自的研究對象.劉老師猜了三句話:“①張博源研究的是莎士比亞;②劉雨恒研究的肯定不是曹雪芹;③高家銘自然不會研究莎士比亞.”很可惜,劉老師的這種猜法,只猜對了一句.據此可以推知張博源、高家銘和劉雨恒分別研究的是__________.(A莎士比亞、B雨果、C曹雪芹,按順序填寫字母即可.)
查看答案和解析>>
科目:高中數學 來源: 題型:
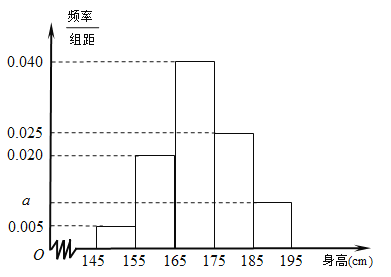
【題目】某中學隨機選取了![]() 名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
(Ⅰ)求![]() 的值及樣本中男生身高在
的值及樣本中男生身高在![]() (單位:
(單位: ![]() )的人數;
)的人數;
(Ⅱ)假設同一組中的每個數據可用該組區間的中點值代替,通過樣本估計該校全體男生的平均身高;
(Ⅲ)在樣本中,從身高在![]() 和
和![]() (單位:
(單位: ![]() )內的男生中任選兩人,求這兩人的身高都不低于
)內的男生中任選兩人,求這兩人的身高都不低于![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|2x+![]() |+a|x﹣
|+a|x﹣![]() |.
|.
(Ⅰ)當a=﹣1時,解不等式f(x)≤3x;
(Ⅱ)當a=2時,若關于x的不等式2f(x)+1<|1﹣b|的解集為空集,求實數b的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱ABC﹣A1B1C1中,側面ABB1A1⊥底面ABC,CA=CB,D,E,F分別為AB,A1D,A1C的中點,點G在AA1上,且A1D⊥EG. 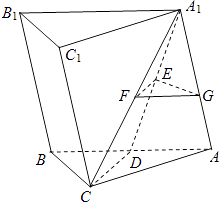
(1)求證:CD∥平面EFG;
(2)求證:A1D⊥平面EFG.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足an+1+an=4n﹣3,n∈N*
(1)若數列{an}是等差數列,求a1的值;
(2)當a1=﹣3時,求數列{an}的前n項和Sn;
(3)若對任意的n∈N* , 都有 ![]() ≥5成立,求a1的取值范圍.
≥5成立,求a1的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com