
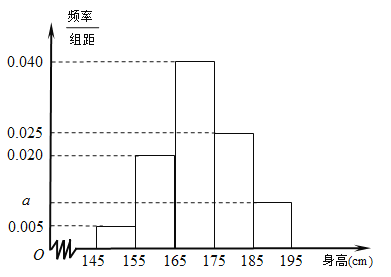
【題目】某中學隨機選取了![]() 名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
名男生,將他們的身高作為樣本進行統計,得到如圖所示的頻率分布直方圖.觀察圖中數據,完成下列問題.
(Ⅰ)求![]() 的值及樣本中男生身高在
的值及樣本中男生身高在![]() (單位:
(單位: ![]() )的人數;
)的人數;
(Ⅱ)假設同一組中的每個數據可用該組區間的中點值代替,通過樣本估計該校全體男生的平均身高;
(Ⅲ)在樣本中,從身高在![]() 和
和![]() (單位:
(單位: ![]() )內的男生中任選兩人,求這兩人的身高都不低于
)內的男生中任選兩人,求這兩人的身高都不低于![]() 的概率.
的概率.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】試題分析:(1)根據頻率直方圖的總面積為1,可求得![]() ,n=N*高*組距
,n=N*高*組距![]() 。(2)平均數為,每個區間的中點值與頻率乘積和。
。(2)平均數為,每個區間的中點值與頻率乘積和。
(3)學生身高在![]() 內的人有
內的人有![]() 個,記這四人為
個,記這四人為![]() .所以,身高在
.所以,身高在![]() 和
和![]() 內的男生共
內的男生共![]() 人。采用枚舉可得總共15個基本事件,滿足的有6個。
人。采用枚舉可得總共15個基本事件,滿足的有6個。![]() 。
。
試題解析:(Ⅰ)根據題意, ![]() .
.
解得 ![]() .
.
所以樣本中學生身高在![]() 內(單位:
內(單位: ![]() )的人數為
)的人數為
![]() .
.
(Ⅱ)設樣本中男生身高的平均值為![]() ,則
,則
![]()
![]() .
.
所以,該校男生的平均身高為![]() .
.
(Ⅲ)樣本中男生身高在![]() 內的人有
內的人有
![]() (個),記這兩人為
(個),記這兩人為![]() .
.
由(Ⅰ)可知,學生身高在![]() 內的人有
內的人有![]() 個,記這四人為
個,記這四人為![]() .
.
所以,身高在![]() 和
和![]() 內的男生共
內的男生共![]() 人.
人.
從這![]() 人中任意選取
人中任意選取![]() 人,有
人,有![]() ,
,
共![]() 種情況.
種情況.
設所選兩人的身高都不低于![]() 為事件
為事件![]() ,事件
,事件![]() 包括
包括![]() ,共
,共![]() 種情況.
種情況.
所以,所選兩人的身高都不低于![]() 的概率為
的概率為![]() .
.


 輕松課堂單元期中期末專題沖刺100分系列答案
輕松課堂單元期中期末專題沖刺100分系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex , 對于實數m、n、p有f(m+n)=f(m)+f(n),f(m+n+p)=f(m)+f(n)+f(p),則p的最大值等于 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
, ![]()
![]() .
.
(Ⅰ)若直線![]()
![]() 與曲線
與曲線![]() 和
和![]() 分別交于
分別交于![]() 兩點.設曲線
兩點.設曲線
![]() 在點
在點![]() 處的切線為
處的切線為![]() ,
, ![]() 在點
在點![]() 處的切線為
處的切線為![]() .
.
(ⅰ)當![]() 時,若
時,若![]()
![]() ,求
,求![]() 的值;
的值;
(ⅱ)若![]() ,求
,求![]() 的最大值;
的最大值;
(Ⅱ)設函數![]() 在其定義域內恰有兩個不同的極值點
在其定義域內恰有兩個不同的極值點![]() ,
, ![]() ,且
,且![]() .
.
若![]() ,且
,且![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn , a1=﹣ ![]() ,Sn+
,Sn+ ![]() =an﹣2(n≥2,n∈N)
=an﹣2(n≥2,n∈N)
(1)求S2 , S3 , S4的值;
(2)猜想Sn的表達式;并用數學歸納法加以證明.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查高中生的數學成績與學生自主學習時間之間的相關關系,長郡中學數學教師對新入學的45名學生進行了跟蹤調查,其中每周自主做數學題的時間不少于15小時的有19人,余下的人中,在高三模擬考試中數學平均成績不足120分的占![]() ,統計成績后,得到如下的
,統計成績后,得到如下的![]() 列聯表:
列聯表:
分數大于等于120分 | 分數不足120分 | 合計 | |
周做題時間不少于15小時 | 4 | 19 | |
周做題時間不足15小時 | |||
合計 | 45 |
(1)請完成上面的![]() 列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“高中生的數學成績與學生自主學習時間有關”;
列聯表,并判斷能否在犯錯誤的概率不超過0.01的前提下認為“高中生的數學成績與學生自主學習時間有關”;
(2)(ⅰ)按照分層抽樣的方法,在上述樣本中,從分數大于等于120分和分數不足120分兩組學生中抽取9名學生,設抽到的不足120分且周做題時間不足15小時的人數是![]() ,求
,求![]() 的分布列(概率用組合數算式表示);
的分布列(概率用組合數算式表示);
(ⅱ)若將頻率視為概率,從全校大于等于120分的學生中隨機抽取20人,求這些人中周做題時間不少于15小時的人數的期望和方差.
|
|
|
|
|
|
|
|
附: 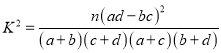
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在長方體ABCD﹣A1B1C1D1中,AA1=AD=1,E為CD中點. 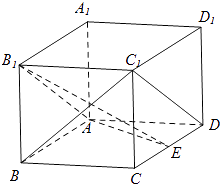
(1)求證:C1D∥平面AB1E;
(2)求證:BC1⊥B1E;
(3)若AB= ![]() ,求二面角E﹣AB1﹣B的正切值.
,求二面角E﹣AB1﹣B的正切值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com