
(1)寫出fk(1);
(2)證明:對任意的x1,x2∈[-1,1],恒有|F(x1)-F(x2)|≤2n-1(n+2)-n-1.
(1)解:由已知推得fk(x)=(n-k+1)·xn-k,從而有fk(1)=n-k+1.
(2)證明:證法1:當-1≤x≤1時,
F(x)=x2n+n![]() x2(n-1)+(n-1)·
x2(n-1)+(n-1)·![]() x2(n-2)+…+(n-k+1)
x2(n-2)+…+(n-k+1)![]() x2(n-k)+…+2
x2(n-k)+…+2![]() nx2+1,
nx2+1,
當x>0時,F(xiàn)′(x)>0,所以F(x)在[0,1]上為增函數(shù).
因函數(shù)F(x)為偶函數(shù),所以F(x)在[-1,0]上為減函數(shù).
所以對任意的x1,x2∈[-1,1],|F(x1)-F(x2)|≤F(1)-F(0).
F(1)-F(0)==![]() +n
+n![]() +(n-1)
+(n-1)![]() +…+(n-k+1)
+…+(n-k+1)![]() +…+2
+…+2![]()
=n![]() n+(n-1)
n+(n-1)![]() +…+(n-k+1)·
+…+(n-k+1)·![]() +…+2
+…+2![]() +=
+=![]() .
.
∵(n-k+1)![]() =(n-k)
=(n-k)![]() n+
n+![]() n=n
n=n![]() +
+![]() n(k=1,2,3…n-1),
n(k=1,2,3…n-1),
F(1)-F(0)=n(![]() +
+![]() +…+
+…+![]() )+(
)+(![]() +
+![]() …+
…+![]() n)+
n)+![]()
=n(2n-1-1)+2n-1=2n-1(n+2)-n-1.
因此結論成立.
證法2:當-1≤x≤1時,
F(x)=x2n+n![]() x2(n-1)+(n-1)·
x2(n-1)+(n-1)·![]() x2(n-2)+…+(n-k+1)
x2(n-2)+…+(n-k+1)![]() x2(n-2)+…+2
x2(n-2)+…+2![]() nx2+1,
nx2+1,
當x>0時,F(xiàn)′(x)>0,所以F(x)在[0,1]上為增函數(shù).
因函數(shù)F(x)為偶函數(shù),所以F(x)在[-1,0]上為減函數(shù).
所以對任意的x1,x2∈[-1,1],|F(x1)-F(x2)|<F(1)-F(0).
F(1)-F(0)= ![]() +n
+n![]() +(n-1)
+(n-1)![]() +…+(n-k+1)
+…+(n-k+1)![]() +…+2
+…+2![]() .
.
又因F(1)-F(0)=2![]() +3
+3![]() +…+k
+…+k![]() +…+n
+…+n![]() n+
n+![]() ,
,
所以2[F(1)-F(0)]=(n+2)[![]() +
+![]() +…+
+…+![]() +…+
+…+![]() ]+2
]+2![]() .
.
F(1)-F(0)=+![]() [
[![]() +
+![]() +…+
+…+![]() +…+
+…+![]() ]+
]+![]() =
=
![]() (2n-2)+1=2n-1(n+2)-n-1.
(2n-2)+1=2n-1(n+2)-n-1.
因此結論成立.
證法3:當-1≤x≤1時,
F(x)=x2n+n![]() x 2(n-1)+(n-1)
x 2(n-1)+(n-1)![]() nx2(n-2)+…+(n-k+1)·
nx2(n-2)+…+(n-k+1)·![]() x2(n-k)+…+2
x2(n-k)+…+2![]() nx2+1,
nx2+1,
當x>0時,F(xiàn)′(x)>0,所以F(x)在[0,1]上為增函數(shù).
因函數(shù)F(x)為偶函數(shù),所以F(x)在[-1,0]上為減函數(shù).
所以對任意的x1,x2∈[-1,1],|F(x1)-F(x2)|≤F(1)-F(0).
F(1)-F(0)=![]() +n
+n![]() +(n-1)
+(n-1)![]() +…+(n-k+1)
+…+(n-k+1)![]() +…+2
+…+2![]()
x[(1+x)n-xn]=x[![]() xn-1+
xn-1+![]() xn-2+…+
xn-2+…+![]() xn-k+…+
xn-k+…+![]() x+1]
x+1]
=![]() xn+
xn+![]() xn-1+…+
xn-1+…+![]() xn-k+1+…+
xn-k+1+…+![]() x2+x,
x2+x,
對上式兩邊求導得
(1+x)n-xn+nx(1+x)n-1-nxn=n![]() xn-1+(n-1)
xn-1+(n-1)![]() xn-2+…(n-k+1)·
xn-2+…(n-k+1)·![]() xn-k+…+2
xn-k+…+2![]() x+1.
x+1.
F(x)=(1+x2)n+nx2(1+x2)n-1-nx 2n,∴F(1)-F(0)=2n+n2n-1-n-1=(n+2)2n-1-n-1.
因此結論成立.


科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學 來源:遼寧省高考真題 題型:解答題
 ,其中k≤n(n,k∈N+),設F(x)=
,其中k≤n(n,k∈N+),設F(x)=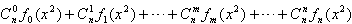 ,x∈[-1,1]。
,x∈[-1,1]。查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com