【答案】
分析:(1)由已知中
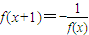
,可得
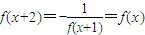
,進而結合f(x)+f(2-x)=0,可得f(x)+f(-x)=0,結合奇函數的定義,可得答案.
(2)由已知中當
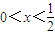
時,f(x)=3
x.結合(1)中結論,可得f(x)在區間
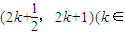
Z)上的解析式;
(3)由(2)的結論及指數的運算性質,我依次為可將不等式log
3f(x)>x
2-kx-2k轉化為二次不等式的形式,進而分析出對應函數在區間
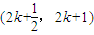
上的單調性,即可得到結論.
解答:解:(1)由
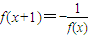
得
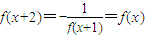
,(3分)
由f(x)+f(2-x)=0得f(x)+f(-x)=0,(4分)
故f(x)是奇函數.(5分)
(2)當x∈
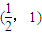
時,
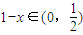
,
∴f(1-x)=3
1-x. (7分)
而
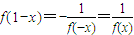
,
∴f(x)=3
x-1. (9分)
當x∈
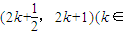
Z)時,
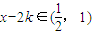
,
∴f(x-2k)=3
x-2k-1,
因此f(x)=f(x-2k)=3
x-2k-1. (11分)
(3)不等式log
3f(x)>x
2-kx-2k即為x-2k-1>x
2-kx-2k,
即x
2-(k+1)x+1<0. (13分)
令g(x)=x
2-(k+1)x+1,對稱軸為
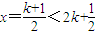
,
因此函數g(x)在
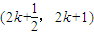
上單調遞增. (15分)
因為
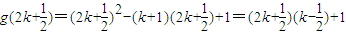
,又k為正整數,
所以
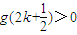
,因此x
2-(k+1)x+1>0在
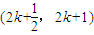
上恒成立,(17分)
因此不存在正整數k使不等式有解. (18分)
點評:本題考查的知識點是對數函數圖象與性質的綜合應用,其中(1)的關鍵由已知條件得到f(x)+f(-x)=0,(2)的關鍵是由已知判斷出f(x)=f(x-2k),(3)的關鍵是根據(2)的結論構造關于k的不等式.

 且f(x)+f(2-x)=0,
且f(x)+f(2-x)=0,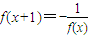 ,當
,當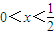 時,f(x)=3x.
時,f(x)=3x. Z)上的解析式;
Z)上的解析式;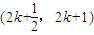 時,不等式log3f(x)>x2-kx-2k有解?證明你的結論.
時,不等式log3f(x)>x2-kx-2k有解?證明你的結論.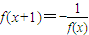 ,可得
,可得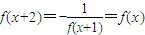 ,進而結合f(x)+f(2-x)=0,可得f(x)+f(-x)=0,結合奇函數的定義,可得答案.
,進而結合f(x)+f(2-x)=0,可得f(x)+f(-x)=0,結合奇函數的定義,可得答案.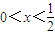 時,f(x)=3x.結合(1)中結論,可得f(x)在區間
時,f(x)=3x.結合(1)中結論,可得f(x)在區間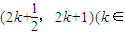 Z)上的解析式;
Z)上的解析式;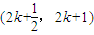 上的單調性,即可得到結論.
上的單調性,即可得到結論.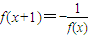 得
得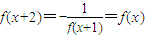 ,(3分)
,(3分)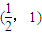 時,
時,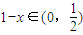 ,
,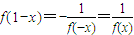 ,
,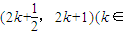 Z)時,
Z)時,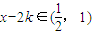 ,
,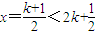 ,
,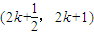 上單調遞增. (15分)
上單調遞增. (15分)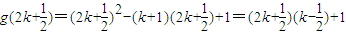 ,又k為正整數,
,又k為正整數,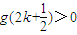 ,因此x2-(k+1)x+1>0在
,因此x2-(k+1)x+1>0在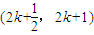 上恒成立,(17分)
上恒成立,(17分)

 名校課堂系列答案
名校課堂系列答案