
 ,則sin2x的值等于( )
,則sin2x的值等于( )



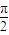 +2x)=-sin2x得到sin2x=-cos2(x+
+2x)=-sin2x得到sin2x=-cos2(x+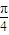 ),然后利用二倍角的余弦函數公式化簡為關于sin(x+
),然后利用二倍角的余弦函數公式化簡為關于sin(x+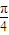 )的關系式,將已知條件代入即可求出值.
)的關系式,將已知條件代入即可求出值.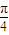 )=
)=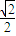 (sinx+cosx)=-
(sinx+cosx)=-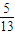 ,
, (1+2sinxcosx)=
(1+2sinxcosx)=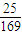 ,
,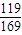 ,
,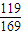 ;
;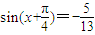 ,
,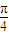 )=-[1-2sin2(x+
)=-[1-2sin2(x+ )]=-
)]=-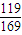 .
.

 通城學典默寫能手系列答案
通城學典默寫能手系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com