
【題目】一個函數![]() ,如果對任意一個三角形,只要它的三邊長
,如果對任意一個三角形,只要它的三邊長![]() 、
、![]() 、
、![]() 都在
都在![]() 的定義域內,就有
的定義域內,就有![]() 、
、![]() 、
、![]() 也是某個三角形的三邊長,則稱
也是某個三角形的三邊長,則稱![]() 為“雙三角形函數”.
為“雙三角形函數”.
(1)判斷![]() ,
,![]() ,
,![]() 中,哪些是“雙三角形函數”,哪些不是,并說明理由;
中,哪些是“雙三角形函數”,哪些不是,并說明理由;
(2)若![]() 是定義在
是定義在![]() 上周期函數,值域為
上周期函數,值域為![]() ,求證:
,求證:![]() 不是“雙三角形函數”;
不是“雙三角形函數”;
(3)已知函數![]() ,
,![]() ,求證:函數
,求證:函數![]() 是“雙三角形函數”.(可利用公式“
是“雙三角形函數”.(可利用公式“![]() ”)
”)
【答案】(1)![]() 、
、![]() 是“雙三角形函數”,
是“雙三角形函數”,![]() 不是;(2)證明見解析;(3)證明見解析.
不是;(2)證明見解析;(3)證明見解析.
【解析】
(1)任給三角形,設它的三邊長分別為![]() 、
、![]() 、
、![]() ,則
,則![]() ,不妨設
,不妨設![]() ,判斷
,判斷![]() 、
、![]() 、
、![]() 是否滿足任意兩數之和大于第三個數,即任意兩邊之和大于第三邊;
是否滿足任意兩數之和大于第三個數,即任意兩邊之和大于第三邊;
(2)要想一個函數不是“雙三角形函數”關鍵是根據題中條件![]() 是定義在
是定義在![]() 上的周期函數,值域為
上的周期函數,值域為![]() ,舉出反例;
,舉出反例;
(3)分別討論![]() 與
與![]() 兩種情況下
兩種情況下![]() 的關系,即可得證
的關系,即可得證
(1)![]() 、
、![]() 是“雙三角形函數”,
是“雙三角形函數”,![]() 不是;
不是;
任給三角形,設它的三邊長分別為![]() 、
、![]() 、
、![]() ,則
,則![]() ,不妨設
,不妨設![]() ,由于
,由于![]() ,所以
,所以![]() 、
、![]() 是“雙三角形函數”.
是“雙三角形函數”.
對于![]() ,3,3,5可以作為一個三角形的三邊長,但
,3,3,5可以作為一個三角形的三邊長,但![]() ,所以不存在三角形以
,所以不存在三角形以![]() 可作為一個三角形的三邊長,故
可作為一個三角形的三邊長,故![]() 不是“雙三角形函數”.
不是“雙三角形函數”.
(2)證明:設![]() 為
為![]() 的一個周期,由于其值域為
的一個周期,由于其值域為![]() ,所以,存在
,所以,存在![]() ,使得
,使得![]() ,
,![]() ,取正整數
,取正整數![]() ,可知
,可知![]() ,
,![]() ,
,![]() 這三個數可作為一個三角形的三邊長,但
這三個數可作為一個三角形的三邊長,但![]() ,
,![]() ,
,![]() 不能作為任何一個三角形的三邊長,故
不能作為任何一個三角形的三邊長,故![]() 不是“雙三角形函數”.
不是“雙三角形函數”.
(3)證明:對任意三角形的三邊![]() 、
、![]() 、
、![]() ,若
,若![]() ,
,
則①當![]() 時,此時
時,此時![]() ,同理可得
,同理可得![]() ,
,![]() ,
,
所以![]() ,則
,則![]() ,
,![]() ,同理可證其余兩式.
,同理可證其余兩式.
所以![]() 可作為某個三角形的三邊長.
可作為某個三角形的三邊長.
②![]() ,此時
,此時![]() ,可得如下兩種情況:
,可得如下兩種情況:
當![]() 時,由于
時,由于![]() ,所以
,所以![]() .
.
由![]() 在
在![]() 上的單調性可得
上的單調性可得![]() ;
;
當![]() 時,
時,![]() ,同樣,由
,同樣,由![]() 在
在![]() 上的單調性可得
上的單調性可得![]()
故![]() ,
,
又由![]() 及余弦函數在
及余弦函數在![]() 上單調遞減,可得
上單調遞減,可得![]() ,
,
所以![]() ,
,
同理可證其余兩式,所以![]() 可作為某個三角形的三邊長.
可作為某個三角形的三邊長.
綜上,函數![]() 是“雙三角形函數”.
是“雙三角形函數”.


 新課標同步訓練系列答案
新課標同步訓練系列答案 一線名師口算應用題天天練一本全系列答案
一線名師口算應用題天天練一本全系列答案科目:高中數學 來源: 題型:
【題目】由9個正數組成的矩陣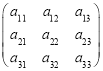 中,每行中三個數成等差數列,且
中,每行中三個數成等差數列,且![]() 、
、![]() 、
、![]() 成等比數列,給出下列判斷:① 第2列中,
成等比數列,給出下列判斷:① 第2列中,![]() 、
、![]() 、
、![]() 必成等比數列;② 第1列中的
必成等比數列;② 第1列中的![]() 、
、![]() 、
、![]() 不一定成等比數列;③
不一定成等比數列;③ ![]() ;④ 若9個數之和等于9,則
;④ 若9個數之和等于9,則![]() ;其中正確的個數為( )
;其中正確的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() 其右頂點為
其右頂點為![]() ,下頂點為
,下頂點為![]() ,定點
,定點![]() ,
,![]() 的面積為
的面積為![]() 過點
過點![]() 作與
作與![]() 軸不重合的直線
軸不重合的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,直線
兩點,直線![]() 分別與
分別與![]() 軸交于
軸交于![]() 兩點.
兩點.

(1)求橢圓![]() 的方程;
的方程;
(2)試探究![]() 的橫坐標的乘積是否為定值,說明理由.
的橫坐標的乘積是否為定值,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年1月1日起我國實施了個人所得稅的新政策,其政策的主要內容包括:(1)個稅起征點為5000元;(2)每月應納稅所得額(含稅)![]() 收入
收入![]() 個稅起征點
個稅起征點![]() 專項附加扣除;(3)專項附加扣除包括①贍養老人費用 ②子女教育費用 ③繼續教育費用 ④大病醫療費用
專項附加扣除;(3)專項附加扣除包括①贍養老人費用 ②子女教育費用 ③繼續教育費用 ④大病醫療費用![]() 等,其中前兩項的扣除標準為:①贍養老人費用:每月共扣除2000元 ②子女教育費用:每個子女每月扣除1000元.新個稅政策的稅率表部分內容如下:
等,其中前兩項的扣除標準為:①贍養老人費用:每月共扣除2000元 ②子女教育費用:每個子女每月扣除1000元.新個稅政策的稅率表部分內容如下:
級數 | 全月應納稅所得額 | 稅率 |
1 | 不超過3000元的部分 | 3% |
2 | 超過3000元至12000元的部分 | 10% |
3 | 超過12000元至25000元的部分 | 20% |
|
|
|
現有李某月收入18000元,膝下有兩名子女,需要贍養老人,(除此之外,無其它專項附加扣除,專項附加扣除均按標準的100%扣除),則李某月應繳納的個稅金額為( )
A.590元B.690元C.790元D.890元
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定函數![]() 和
和![]() ,令
,令![]() ,對以下三個論斷:
,對以下三個論斷:
(1)若![]() 和
和![]() 都是奇函數,則
都是奇函數,則![]() 也是奇函數;(2)若
也是奇函數;(2)若![]() 和
和![]() 都是非奇非偶函數,則
都是非奇非偶函數,則![]() 也是非奇非偶函數:(3)
也是非奇非偶函數:(3)![]() 和
和![]() 之一與
之一與![]() 有相同的奇偶性;其中正確論斷的個數為( )
有相同的奇偶性;其中正確論斷的個數為( )
A.0個B.1個C.2個D.3個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() .
.
(1)根據![]() 不同取值,討論函數
不同取值,討論函數![]() 的奇偶性;
的奇偶性;
(2)若![]() ,對于任意的
,對于任意的![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若已知![]() ,
,![]() . 設函數
. 設函數![]() ,
,![]() ,存在
,存在![]() 、
、![]() ,使得
,使得![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com