
【題目】設函數f(x)=xln(x﹣1)﹣a(x﹣2). (Ⅰ)若a=2017,求曲線f(x)在x=2處的切線方程;
(Ⅱ)若當x≥2時,f(x)≥0,求a的取值范圍.
【答案】解:(Ⅰ)a=2017時,f(x)=xln(x﹣1)﹣2017(x﹣2), 則f′(x)=ln(x﹣1)+ ![]() ﹣2017,故f′(2)=﹣2015,
﹣2017,故f′(2)=﹣2015,
又f(2)=0,
故切線方程是:y﹣0=﹣2015(x﹣2),
即2015x+y﹣4030=0;
(Ⅱ)由f(x)≥0得xln(x﹣1)﹣a(x﹣2)≥0,而x≥2,
故ln(x﹣1)﹣ ![]() ≥0,
≥0,
設函數g(x)=ln(x﹣1)﹣ ![]() ,(x≥2),
,(x≥2),
于是問題轉化為g(x)≥0對任意的x≥2恒成立,
注意到g(2)=0,故若g′(x)≥0,則g(x)遞增,
從而g(x)≥g(2)=0,而g′(x)= ![]() ,
,
∴g′(x)≥0等價于x2﹣2a(x﹣1)≥0,
分離參數得a≤ 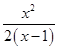 =
= ![]() [(x﹣1)+
[(x﹣1)+ ![]() +2],
+2],
由均值不等式得 ![]() [(x﹣1)+
[(x﹣1)+ ![]() +2]≥2,
+2]≥2,
當且僅當x=2時取“=”成立,于是a≤2,
當a>2時,設h(x)=x2﹣2a(x﹣1),
∵h(2)=4﹣2a=2(2﹣a)>0,
又拋物線h(x)=x2﹣2a(x﹣1)開口向上,
故h(x)=x2﹣2a(x﹣1)有2個零點,
設兩個零點為x1 , x2 , 則x1<2<x2 ,
于是x∈(2,x2)時,h(x)<0,故g′(x)<0,g(x)遞減,
故g(x)<g(2)=0,與題設矛盾,不合題意,
綜上,a的范圍是(﹣∞,2].
【解析】(Ⅰ)求出函數的導數,計算f(2),f′(2),求出切線方程即可;(Ⅱ)設函數g(x)=ln(x﹣1)﹣ ![]() ,(x≥2),于是問題轉化為g(x)≥0對任意的x≥2恒成立,根據函數的單調性求出a的范圍即可.
,(x≥2),于是問題轉化為g(x)≥0對任意的x≥2恒成立,根據函數的單調性求出a的范圍即可.
【考點精析】本題主要考查了函數的最大(小)值與導數的相關知識點,需要掌握求函數![]() 在
在![]() 上的最大值與最小值的步驟:(1)求函數
上的最大值與最小值的步驟:(1)求函數![]() 在
在![]() 內的極值;(2)將函數
內的極值;(2)將函數![]() 的各極值與端點處的函數值
的各極值與端點處的函數值![]() ,
,![]() 比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.
比較,其中最大的是一個最大值,最小的是最小值才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】某軟件公司新開發一款學習軟件,該軟件把學科知識設計為由易到難共12關的闖關游戲.為了激發闖關熱情,每闖過一關都獎勵若干慧幣(一種網絡虛擬幣).該軟件提供了三種獎勵方案:第一種,每闖過一關獎勵40慧幣;第二種,闖過第一關獎勵4慧幣,以后每一關比前一關多獎勵4慧幣;第三種,闖過第一關獎勵0.5慧幣,以后每一關比前一關獎勵翻一番(即增加1倍),游戲規定:闖關者須于闖關前任選一種獎勵方案.
(Ⅰ)設闖過n ( n∈N,且n≤12)關后三種獎勵方案獲得的慧幣依次為An , Bn , Cn , 試求出An , Bn , Cn的表達式;
(Ⅱ)如果你是一名闖關者,為了得到更多的慧幣,你應如何選擇獎勵方案?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數f(x)=cos2x圖象上所有點向右平移 ![]() 個單位長度后得到函數g(x)的圖象,若g(x)在區間[0,a]上單調遞增,則實數a的最大值為( )
個單位長度后得到函數g(x)的圖象,若g(x)在區間[0,a]上單調遞增,則實數a的最大值為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x2+ ![]() +alnx(x>0,a為常數).
+alnx(x>0,a為常數).
(1)討論函數g(x)=f(x)﹣x2的單調性;
(2)對任意兩個不相等的正數x1、x2 , 求證:當a≤0時, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,內角A,B,C所對的邊分別為a,b,c,已知2sin2A+sin(A﹣B)=sinC,且 ![]() . (Ⅰ)求
. (Ⅰ)求 ![]() 的值;
的值;
(Ⅱ)若c=2, ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知平面向量 ![]() ,
, ![]() ,
, ![]() 滿足|
滿足| ![]() |=|
|=| ![]() |=
|= ![]() ,|
,| ![]() |=1,若(
|=1,若( ![]() ﹣
﹣ ![]() )(
)( ![]() ﹣
﹣ ![]() )=0,則|
)=0,則| ![]() ﹣
﹣ ![]() |的取值范圍是( )
|的取值范圍是( )
A.[1,2]
B.[2,4]
C.[ ![]() ﹣1,
﹣1, ![]() +1]
+1]
D.[ ![]() ﹣1,
﹣1, ![]() +1]
+1]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=2cos22x﹣2,給出下列命題: ①β∈R,f(x+β)為奇函數;
②α∈(0, ![]() ),f(x)=f(x+2α)對x∈R恒成立;
),f(x)=f(x+2α)對x∈R恒成立;
③x1 , x2∈R,若|f(x1)﹣f(x2)|=2,則|x1﹣x2|的最小值為 ![]() ;
;
④x1 , x2∈R,若f(x1)=f(x2)=0,則x1﹣x2=kπ(k∈Z).其中的真命題有( )
A.①②
B.③④
C.②③
D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設樣本數據x1 , x2 , …,x10的均值和方差分別為1和4,若yi=xi+a(a為非零常數,i=1,2,…,10),則y1 , y2 , …,y10的均值和方差分別為( )
A.1+a,4
B.1+a,4+a
C.1,4
D.1,4+a
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com