
【題目】已知數(shù)列![]() 滿足
滿足![]() .
.
(1)若![]() ,證明:
,證明:
(i)當(dāng)![]() 時,有
時,有![]() ;
;
(ii)當(dāng)![]() 時,有
時,有![]() .
.
(2)若![]() ,證明:當(dāng)
,證明:當(dāng)![]() 時,有
時,有![]() .
.
【答案】(1)(ⅰ)見解析;(ⅱ)見解析;(2)見解析.
【解析】
因為![]() ,
,
所以,![]() ,即數(shù)列
,即數(shù)列![]() 為遞增數(shù)列.
為遞增數(shù)列.
(1)(ⅰ)由![]() 及
及![]() ,可得
,可得![]() ,
,![]() .
.
于是,當(dāng)![]() 時,
時,![]() .
.
故![]()
![]() .
.
因此,當(dāng)![]() 時,
時,![]() .
.
(ⅱ)因為![]() 時,
時,![]() ,
,
所以,![]() ,
,![]() .
.
由![]() ,可得
,可得
![]() .
.
用數(shù)學(xué)歸納法證明:
![]() .
.
當(dāng)![]() 時,
時,![]() ,結(jié)論成立.
,結(jié)論成立.
假設(shè)結(jié)論對![]() 成立,即
成立,即![]() ,則結(jié)合(ⅰ)的結(jié)論可得
,則結(jié)合(ⅰ)的結(jié)論可得
![]() ,
,
即當(dāng)![]() 時,結(jié)論也成立.
時,結(jié)論也成立.
綜合可知,不等式![]() 對一切
對一切![]() 都成立.
都成立.
因此,當(dāng)![]() 時,
時,
![]() ,
,
即![]() .
.
又![]() ,
,![]() ,則當(dāng)
,則當(dāng)![]() 時,有
時,有
![]() .
.
(2)由于![]() ,而數(shù)列
,而數(shù)列![]() 為遞增數(shù)列,故當(dāng)
為遞增數(shù)列,故當(dāng)![]() 時,有
時,有![]() .
.
由![]() ,可得
,可得
![]() .
.
而![]() ,于是,
,于是,

![]() .
.
下面證明:當(dāng)![]() 時,有
時,有
![]() .
.
根據(jù)![]() 及
及![]() ,計算得
,計算得
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() .
.
故當(dāng)![]() 時,結(jié)論成立.
時,結(jié)論成立.
假設(shè)結(jié)論對![]() 成立,即
成立,即
![]() .
.
因為![]() ,而函數(shù)
,而函數(shù)![]() 在
在![]() 時為增函數(shù),所以,
時為增函數(shù),所以,
![]()
![]() ,
,
即當(dāng)![]() 時,結(jié)論也成立.
時,結(jié)論也成立.
綜合可知,不等式![]() 對一切
對一切![]() 都成立.
都成立.
于是,當(dāng)![]() 時,
時,![]() .
.
故![]() .
.
所以,![]() .
.


 小學(xué)奪冠AB卷系列答案
小學(xué)奪冠AB卷系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】為提高衡水市的整體旅游服務(wù)質(zhì)量,市旅游局舉辦了旅游知識競賽,參賽單位為本市內(nèi)各旅游協(xié)會,參賽選手為持證導(dǎo)游.現(xiàn)有來自甲旅游協(xié)會的導(dǎo)游3名,其中高級導(dǎo)游2名;乙旅游協(xié)會的導(dǎo)游3名,其中高級導(dǎo)游1名.從這6名導(dǎo)游中隨機選擇2人參加比賽.
(1)求選出的2名都是高級導(dǎo)游的概率;
(2)為了進一步了解各旅游協(xié)會每年對本地經(jīng)濟收入的貢獻情況,經(jīng)多次統(tǒng)計得到,甲旅游協(xié)會對本地經(jīng)濟收入的貢獻范圍是![]() (單位:萬元),乙旅游協(xié)會對本地經(jīng)濟收入的貢獻范圍是
(單位:萬元),乙旅游協(xié)會對本地經(jīng)濟收入的貢獻范圍是![]() (單位:萬元),求甲旅游協(xié)會對本地經(jīng)濟收入的貢獻不低于乙旅游協(xié)會對本地經(jīng)濟收入的貢獻概率.
(單位:萬元),求甲旅游協(xié)會對本地經(jīng)濟收入的貢獻不低于乙旅游協(xié)會對本地經(jīng)濟收入的貢獻概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)![]() :實數(shù)
:實數(shù)![]() 滿足不等式
滿足不等式![]() ,
,![]() :函數(shù)
:函數(shù)![]() 無極值點.
無極值點.
(1)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數(shù)
”為真命題,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若“![]() 為真命題”是“
為真命題”是“![]() ”的必要不充分條件,求正整數(shù)
”的必要不充分條件,求正整數(shù)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)y=f(x),若在其定義域內(nèi)存在x0,使得x0f(x0)=1成立,則稱函數(shù)f(x)具有性質(zhì)M.
(1)下列函數(shù)中具有性質(zhì)M的有____
①f(x)=﹣x+2
②f(x)=sinx(x∈[0,2π])
③f(x)=x![]() ,(x∈(0,+∞))
,(x∈(0,+∞))
④f(x)![]()
(2)若函數(shù)f(x)=a(|x﹣2|﹣1)(x∈[﹣1,+∞))具有性質(zhì)M,則實數(shù)a的取值范圍是____.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() ,
,![]() .
.
(1)若曲線![]() 與
與![]() 在點
在點![]() 處有相同的切線,求函數(shù)
處有相同的切線,求函數(shù)![]() 的極值;
的極值;
(2)若![]() ,討論函數(shù)
,討論函數(shù)![]() 的單調(diào)性.
的單調(diào)性.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給定平面上的五個點A、B、C、D、E,任意三點不共線.由這些點連成4條線,每點至少是一條線段的端點,不同的聯(lián)結(jié)方式有 種.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】函數(shù)![]() 的圖象如圖所示,為了得到函數(shù)
的圖象如圖所示,為了得到函數(shù)![]() 的圖象,可以把函數(shù)
的圖象,可以把函數(shù)![]() 的圖象( )
的圖象( )
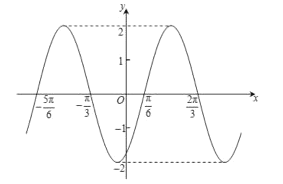
A.先向左平移![]() 個單位,再把所得各點的橫坐標(biāo)伸長到原來的
個單位,再把所得各點的橫坐標(biāo)伸長到原來的![]() 倍(縱坐標(biāo)不變)
倍(縱坐標(biāo)不變)
B.先向左平移![]() 個單位,再把所得各點的橫坐標(biāo)縮短到原來的
個單位,再把所得各點的橫坐標(biāo)縮短到原來的![]() (縱坐標(biāo)不變)
(縱坐標(biāo)不變)
C.每個點的橫坐標(biāo)縮短到原來的![]() (縱坐標(biāo)不變),再向左平移
(縱坐標(biāo)不變),再向左平移![]() 個單位
個單位
D.每個點的橫坐標(biāo)伸長到原來的![]() 倍(縱坐標(biāo)不變),再向左平移
倍(縱坐標(biāo)不變),再向左平移![]() 個單位
個單位
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com