
【題目】已知![]() ,函數
,函數![]() ,直線l:
,直線l:![]() .
.
![]() 討論
討論![]() 的圖象與直線l的交點個數;
的圖象與直線l的交點個數;
![]() 若函數
若函數![]() 的圖象與直線l:
的圖象與直線l:![]() 相交于
相交于![]() ,
,![]() 兩點
兩點![]() ,證明:
,證明:![]() .
.
【答案】(1)見解析(2)見證明
【解析】
![]() 根據函數與方程的關系,設
根據函數與方程的關系,設![]() ,求函數的導數,研究函數的單調性和極值,結合極值與0的關系進行判斷即可.
,求函數的導數,研究函數的單調性和極值,結合極值與0的關系進行判斷即可.
![]() 構造函數
構造函數![]() ,求函數的導數,結合
,求函數的導數,結合![]() 與l的交點坐標,進行證明即可.
與l的交點坐標,進行證明即可.
解:![]() 由題意,令
由題意,令![]() ,
,![]()
則![]() ,
,
令![]() ,解得
,解得![]() .
.
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
令![]() ,解得
,解得![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,
則當![]() 時,函數取得極小值,同時也是最小值
時,函數取得極小值,同時也是最小值
![]() ,
,
![]() 當
當![]() ,即
,即![]() 時,
時,![]() 的圖象與直線l無交點,
的圖象與直線l無交點,
![]() 當
當![]() ,即
,即![]() 時
時![]() 的圖象與直線l只有一個交點.
的圖象與直線l只有一個交點.
![]() 當
當![]() ,即
,即![]() 時
時![]() 的圖象與直線l有兩個交點.
的圖象與直線l有兩個交點.
綜上所述,當![]() 時,
時,![]() 的圖象與直線l無交點;
的圖象與直線l無交點;
![]() 時
時![]() 的圖象與直線l只有一個交點,
的圖象與直線l只有一個交點,![]() 時
時![]() 的圖象與直線l有兩個交點.
的圖象與直線l有兩個交點.
![]() 證明:令
證明:令![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() ,即
,即![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ,
,
![]() 時,
時,![]() 恒成立,
恒成立,
又![]() ,
,
![]() ,
,
![]() ,
,
又![]()
![]() ,
,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() 即
即![]()
![]() .
.


科目:高中數學 來源: 題型:
【題目】一個生產公司投資A生產線500萬元,每萬元可創造利潤![]() 萬元,該公司通過引進先進技術,在生產線A投資減少了x萬元,且每萬元的利潤提高了
萬元,該公司通過引進先進技術,在生產線A投資減少了x萬元,且每萬元的利潤提高了![]() ;若將少用的x萬元全部投入B生產線,每萬元創造的利潤為
;若將少用的x萬元全部投入B生產線,每萬元創造的利潤為![]() 萬元,其中
萬元,其中![]() .
.
![]() 若技術改進后A生產線的利潤不低于原來A生產線的利潤,求x的取值范圍;
若技術改進后A生產線的利潤不低于原來A生產線的利潤,求x的取值范圍;
![]() 若生產線B的利潤始終不高于技術改進后生產線A的利潤,求a的最大值.
若生產線B的利潤始終不高于技術改進后生產線A的利潤,求a的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的值域為
的值域為![]() ,記函數
,記函數![]() .
.
(1)求實數![]() 的值;
的值;
(2)存在![]() 使得不等式
使得不等式![]() 成立,求實數
成立,求實數![]() 的取值范圍;
的取值范圍;
(3)若關于![]() 的方程
的方程![]() 有5個不等的實數根,求實數
有5個不等的實數根,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:![]() ,直線1過原點O.
,直線1過原點O.
(1)若直線l與圓C相切,求直線l的斜率;
(2)若直線l與圓C交于A、B兩點,點P的坐標為![]() ,若
,若![]() .求直線l的方程.
.求直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列關于復數![]() 的四個命題中,正確的個數是( )
的四個命題中,正確的個數是( )
(1)若![]() ,則復數
,則復數![]() 對應的動點的軌跡是橢圓;
對應的動點的軌跡是橢圓;
(2)若![]() ,則復數
,則復數![]() 對應的動點的軌跡是雙曲線;
對應的動點的軌跡是雙曲線;
(3)若![]() ,則復數
,則復數![]() 對應的動點的軌跡是拋物線;
對應的動點的軌跡是拋物線;
(4)若![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]()
A.4B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠去年某產品的年產量為100萬只,每只產品的銷售價為10元,固定成本為8元![]() 今年,工廠第一次投入100萬元
今年,工廠第一次投入100萬元![]() 科技成本
科技成本![]() ,并計劃以后每年比上一年多投入100萬元
,并計劃以后每年比上一年多投入100萬元![]() 科技成本
科技成本![]() ,預計產量年遞增10萬只,第
,預計產量年遞增10萬只,第![]() 次投入后,每只產品的固定成本為
次投入后,每只產品的固定成本為![]() 為常數,
為常數,![]() 且
且![]() ,若產品銷售價保持不變,第
,若產品銷售價保持不變,第![]() 次投入后的年利潤為
次投入后的年利潤為![]() 萬元.
萬元.
(1)求![]() 的值,并求出
的值,并求出![]() 的表達式;
的表達式;
(2)問從今年算起第幾年利潤最高?最高利潤為多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,曲線C1的參數方程為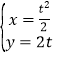 (t為參數),曲線C2的參數方程為
(t為參數),曲線C2的參數方程為![]() (α為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(α為參數),以O為極點,x軸的正半軸為極軸建立極坐標系.
(1)求曲線C1和C2的極坐標方程;
(2)直線l的極坐標方程為![]() ,直線l與曲線C1和C2分別交于不同于原點的A,B兩點,求|AB|的值.
,直線l與曲線C1和C2分別交于不同于原點的A,B兩點,求|AB|的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】摩拜單車和![]() 小黃車等各種共享單車的普及給我們的生活帶來了便利.已知某共享單車的收費標準是:每車使用不超過1小時(包含1小時)是免費的,超過1小時的部分每小時收費1元(不足1小時的部分按1小時計算,例如:騎行2.5小時收費2元).現有甲、乙兩人各自使用該種共享單車一次.設甲、乙不超過1小時還車的概率分別為
小黃車等各種共享單車的普及給我們的生活帶來了便利.已知某共享單車的收費標準是:每車使用不超過1小時(包含1小時)是免費的,超過1小時的部分每小時收費1元(不足1小時的部分按1小時計算,例如:騎行2.5小時收費2元).現有甲、乙兩人各自使用該種共享單車一次.設甲、乙不超過1小時還車的概率分別為![]() 1小時以上且不超過2小時還車的概率分別為
1小時以上且不超過2小時還車的概率分別為![]() 兩人用車時間都不會超過3小時.
兩人用車時間都不會超過3小時.
(Ⅰ)求甲乙兩人所付的車費相同的概率;
(Ⅱ)設甲乙兩人所付的車費之和為隨機變量![]() 求
求![]() 的分布列及數學期望
的分布列及數學期望![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com