【題目】某大型企業針對改善員工福利的
，
，
三種方案進行了問卷調查，調查結果如下：
支持 | 支持 | 支持 | |
35歲以下的人數 | 200 | 400 | 800 |
35歲及以上的人數 | 100 | 100 | 400 |
（1）從所有參與調查的人中，用分層隨機抽樣的方法抽取
人，已知從支持方案的人中抽取了6人，求的值.
（2）從支持方案的人中，用分層隨機抽樣的方法抽取5人，這5人中年齡在35歲及以上的人數是多少？年齡在35歲以下的人數是多少？
全優考典單元檢測卷及歸類總復習系列答案
品學雙優卷系列答案
小學期末沖刺100分系列答案科目：高中數學 來源： 題型：
【題目】據調查，某地區有300萬從事傳統農業的農民，人均年收入6000元，為了增加農民的收入，當地政府積極引進資本，建立各種加工企業，對當地的農產品進行深加工，同時吸收當地部分農民進入加工企業工作，據估計，如果有
萬人進企業工作，那么剩下從事傳統農業的農民的人均年收入有望提高
，而進入企業工作的農民的人均年收入為
元．
（1）在建立加工企業后，多少農民進入企業工作，能夠使剩下從事傳統農業農民的總收入最大，并求出最大值；
（2）為了保證傳統農業的順利進行，限制農民加入加工企業的人數不能超過總人數的
，當地政府如何引導農民，即
取何值時，能使300萬農民的年總收入最大．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】從某學校高三年級共800名男生中隨機抽取50名學生作為樣本測量身高.測量發現被測學生身高全部介于155cm和195cm之間，將測量結果按如下方式分成八組：第一組
；第二組
；…；第八組
.下圖是按上述分組方法得到的頻率分布直方圖的一部分.已知第一組與第八組人數相同，第六組與第八組人數之和為第七組的兩倍.
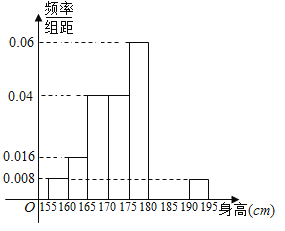
（1）估計這所學校高三年級全體男生身高在180cm以上（含180cm）的人數；
（2）求第六組和第七組的頻率并補充完整頻率分布直方圖.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知梯形
中，
，
，
是
的中點.
，
、
分別是
、
上的動點，且
，設
（
），沿
將梯形翻折，使平面
平面
，如圖.
（1）當
時，求證：
；
（2）若以
、
、
、為頂點的三棱錐的體積記為
，求的最大值；
（3）當取得最大值時，求二面角
的余弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知直線l1：x-2y+3=0與直線l2：2x+3y-8=0的交點為M，
（1）求過點M且到點P（0，4）的距離為2的直線l的方程；
（2）求過點M且與直線l3：x+3y+1=0平行的直線l的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知圓
，直線
， 
.
（1）求證：對
，直線
與圓
總有兩個不同的交點
；
（2）求弦
的中點
的軌跡方程，并說明其軌跡是什么曲線；
（3）是否存在實數
，使得原
上有四點到直線
的距離為
？若存在，求出
的范圍；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2012年，在“雜交水稻之父”袁隆平的實驗田內種植了
，
兩個品種的水稻，為了篩選出更優的品種，在，兩個品種的實驗田中分別抽取7塊實驗田，如圖所示的莖葉圖記錄了這14塊實驗田的畝產量（單位：
），通過莖葉圖比較兩個品種的均值及方差，并從中挑選一個品種進行以后的推廣，有如下結論：①品種水稻的平均產量高于品種水稻，推廣品種水稻；②品種水稻的平均產量高于品種水稻，推廣品種水稻；③品種水稻比品種水稻產量更穩定，推廣品種水稻；④品種水稻比品種水稻產量更穩定，推廣品種水稻；其中正確結論的編號為( )
A.①②B.①③C.②④D.①④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設橢圓C：
的一個頂點與拋物線：
的焦點重合，
分別是橢圓的左、右焦點，離心率
，過橢圓右焦點
的直線l與橢圓C交于M、N兩點．
（1）求橢圓C的方程；
（2）是否存在直線l，使得
，若存在，求出直線l的方程；若不存在，說明理由；
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
