
【題目】在直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在極坐標系中,圓C的極坐標方程為:
為參數),在極坐標系中,圓C的極坐標方程為:![]()
(1)求圓C的直角坐標方程;
(2)設圓C與直線![]() 交于
交于![]() 兩點,若點的坐標為
兩點,若點的坐標為![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)![]() ; (2)
; (2)![]() .
.
【解析】
(1)利用極坐標公式把圓C的極坐標方程化為直角坐標方程.(2) 將l的參數方程代入圓C的直角坐標方程,得t2+2(cos α-sin α)t-7=0,利用弦長公式求出|PA|+|PB|=|t1|+|t2|=|t1-t2|=![]() ,再求其最小值.
,再求其最小值.
(1)由ρ=6sin θ得ρ2=6ρsin θ,化為直角坐標方程為x2+y2=6y,即x2+(y-3)2=9.
所以圓C的直角坐標方程為x2+(y-3)2=9.
(2)將l的參數方程代入圓C的直角坐標方程,得t2+2(cos α-sin α)t-7=0.
由已知得Δ=(2cos α-2sin α)2+4×7>0,
所以可設t1,t2是上述方程的兩根,則![]()
由題意得直線l過點(1,2),結合t的幾何意義得|PA|+|PB|=|t1|+|t2|=|t1-t2|
=![]() =
=![]() =
=![]() ≥
≥![]() =2
=2![]() .
.
所以|PA|+|PB|的最小值為2![]() .
.


 智趣暑假溫故知新系列答案
智趣暑假溫故知新系列答案 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案科目:高中數學 來源: 題型:
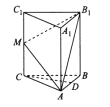
【題目】如圖,在三棱柱![]() 中,側棱
中,側棱![]() 底面
底面![]() ,且
,且![]() ,
, ![]() 是棱
是棱![]() 的中點,點
的中點,點![]() 在側棱
在側棱![]() 上運動.
上運動.
(1)當![]() 是棱
是棱![]() 的中點時,求證:
的中點時,求證: ![]() 平面
平面![]() ;
;
(2)當直線![]() 與平面
與平面![]() 所成的角的正切值為
所成的角的正切值為![]() 時,求二面角
時,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列五個命題,其中正確的命題序號是________.
①當![]() 時,函數
時,函數![]() 取得最大值,則
取得最大值,則![]()
②已知菱形![]() ,
,![]() 為
為![]() 的中點,且
的中點,且![]() ,則菱形
,則菱形![]() 面積的最大值為12
面積的最大值為12
③已知二次函數![]() ,如果
,如果![]() 時
時![]() ,則實數
,則實數![]() 的取值范圍是
的取值范圍是![]()
④在三棱錐![]() 中,
中,![]() ,
,![]() ,點
,點![]() 分別是
分別是![]() 的中點,則異面直線
的中點,則異面直線![]() 所成的角的余弦值是
所成的角的余弦值是![]()
⑤數列![]() 滿足
滿足![]() ,且數列
,且數列![]() 的前2010項的和為403,記數列
的前2010項的和為403,記數列![]() ,
,![]() 是數列
是數列![]() 的前
的前![]() 項和,則
項和,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ax2-2x+1.
(1)試討論函數f(x)的單調性;
(2)若![]() ≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達式;
≤a≤1,且f(x)在[1,3]上的最大值為M(a),最小值為N(a),令g(a)=M(a)-N(a),求g(a)的表達式;
(3)在(2)的條件下,求證:g(a)≥![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
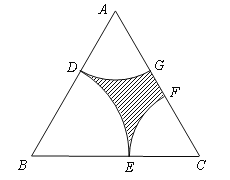
【題目】近年來,隨著我市經濟的快速發展,政府對民生越來越關注市區現有一塊近似正三角形的土地![]() (如圖所示),其邊長為2百米,為了滿足市民的休閑需求,市政府擬在三個頂點處分別修建扇形廣場,即扇形
(如圖所示),其邊長為2百米,為了滿足市民的休閑需求,市政府擬在三個頂點處分別修建扇形廣場,即扇形![]() 和
和![]() ,其中
,其中![]() 與
與![]() 、
、![]() 分別相切于點
分別相切于點![]() ,且
,且![]() 與
與![]() 無重疊,剩余部分(陰影部分)種植草坪.設
無重疊,剩余部分(陰影部分)種植草坪.設![]() 長為
長為![]() (單位:百米),草坪面積為
(單位:百米),草坪面積為![]() (單位:萬平方米).
(單位:萬平方米).
(1)試用![]() 分別表示扇形
分別表示扇形![]() 和
和![]() 的面積,并寫出
的面積,并寫出![]() 的取值范圍;
的取值范圍;
(2)當![]() 為何值時,草坪面積最大?并求出最大面積.
為何值時,草坪面積最大?并求出最大面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知以點![]() 為圓心的圓過原點
為圓心的圓過原點![]() .
.
(1)設直線![]() 與圓
與圓![]() 交于點
交于點![]() ,若
,若![]() ,求圓
,求圓![]() 的方程;
的方程;
(2)在(1)的條件下,設![]() ,且
,且![]() 分別是直線
分別是直線![]() 和圓
和圓![]() 上的動點,求
上的動點,求![]() 的最大值及此時點
的最大值及此時點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設三棱錐![]() 的底面是正三角形,側棱長均相等,
的底面是正三角形,側棱長均相等,![]() 是棱
是棱![]() 上的點(不含端點),記直線
上的點(不含端點),記直線![]() 與直線
與直線![]() 所成角為
所成角為![]() ,直線
,直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,二面角
,二面角![]() 的平面角為
的平面角為![]() ,則( )
,則( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,PA垂直于⊙O所在的平面,M為圓周上任意一點,AN⊥PM,N為垂足.

(1)求證:AN⊥平面PBM;
(2)若AQ⊥PB,垂足為Q,求證:NQ⊥PB.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com